
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)

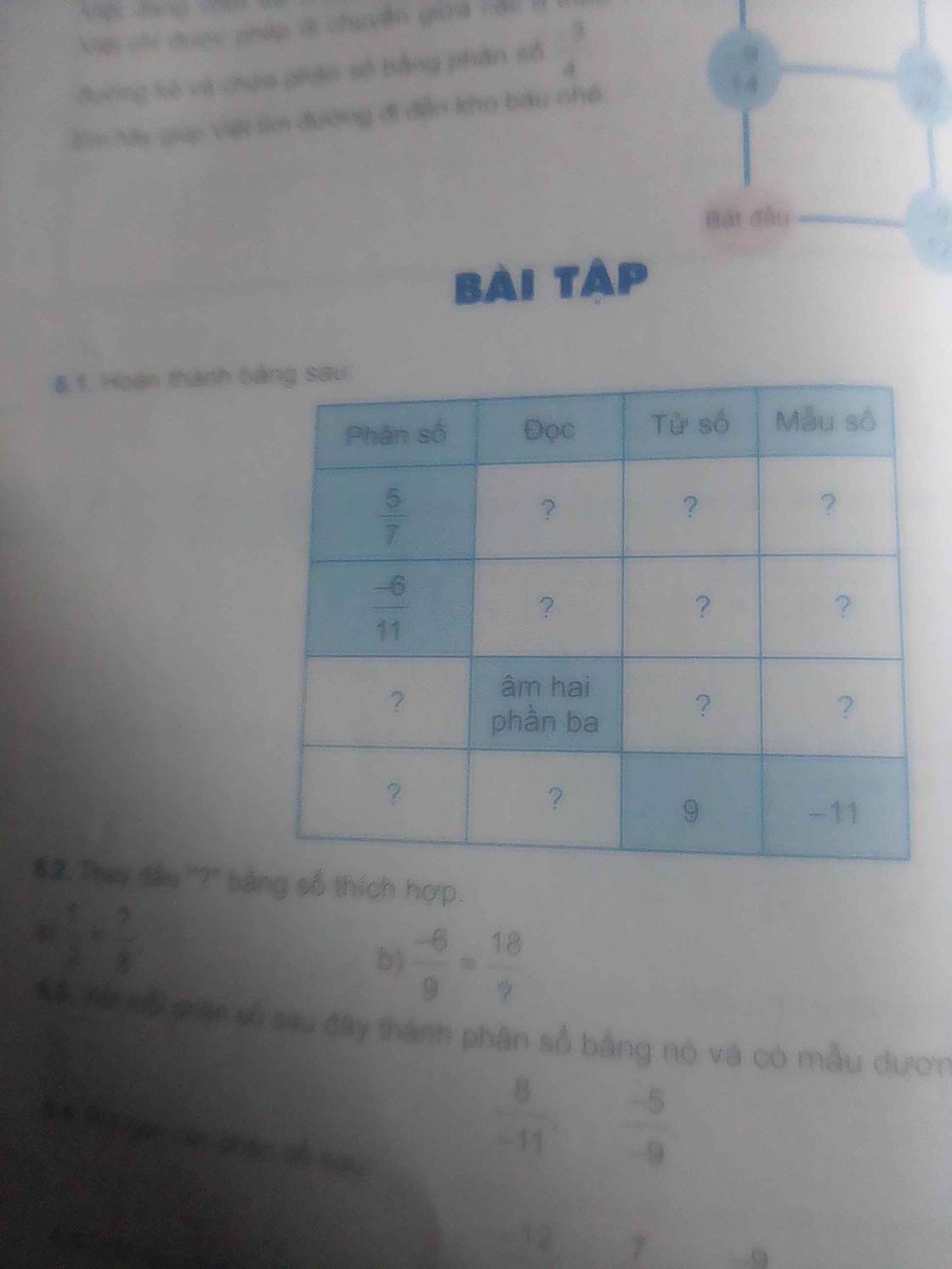
| Phân số | Đọc | Tử Số | Mẫu số |
| \(\dfrac{5}{7}\) | Năm phần bẩy | 5 | 7 |
| \(\dfrac{-6}{11}\) | âm sáu phần mười một | -6 | 11 |
| \(\dfrac{-2}{13}\) | âm hai phần ba | -2 | 13 |
| \(\dfrac{9}{-11}\) | chín phần âm mười một | 9 | -11 |

Bài 4:
\(a,\dfrac{-12}{16}=\dfrac{-12:4}{16:4}=\dfrac{-3}{4};\\ \dfrac{6}{-8}=\dfrac{6:\left(-2\right)}{-8:\left(-2\right)}=\dfrac{-3}{4}\\ Vì:-\dfrac{3}{4}=-\dfrac{3}{4}.Nên:\dfrac{-12}{16}=\dfrac{6}{-8}\\ ---\\ b,.\dfrac{33}{88}=\dfrac{33:11}{88:11}=\dfrac{3}{8}>0;\dfrac{-17}{76}< 0.Nên:-\dfrac{17}{76}< 0< \dfrac{33}{88}.Vậy:\dfrac{-17}{76}\ne\dfrac{33}{88}\)
Mỗi giờ máy bơm thứ nhất bơm vào 1/3 thể tích bể, đồng thời mỗi giờ máy bơm thứ hai hút ra được 1/5 thể tích bể:
Ta có: 1/3 - 1/5 = 5/15 - 3/15 = 2/15 (thể tích bể)
Vậy nếu dùng 2 máy bơm để cùng cấp và thoát nước trong bể 1 giờ thì bể thêm được thể tích là 2/15 bể. Dùng phân số dương nhé!

Bài 2:
a) Có hai đường thẳng trong hình
b) Điểm O không thuộc đường thẳng nào
c) A thuộc đường thẳng c và không thuộc đường thẳng d
d) Các điểm thuộc đường thẳng d là S và B
Các điểm không thuộc đường thẳng d là A và O


\(a,-\dfrac{9}{4}< 0;\dfrac{1}{3}>0.Nên:-\dfrac{9}{4}< \dfrac{1}{3}\\ b,-\dfrac{8}{3}< -2;\dfrac{4}{-7}>-1.Nên:-\dfrac{8}{3}< -2< -1< \dfrac{4}{-7}\\ Vậy:-\dfrac{8}{3}< \dfrac{4}{-7}\\ c,\dfrac{9}{-5}< -1;\dfrac{7}{-10}>-1.Nên:\dfrac{9}{-5}< -1< \dfrac{7}{-10}.Vậy:\dfrac{9}{-5}< \dfrac{7}{-10}\\ d,\dfrac{3}{14}>0;-\dfrac{6}{14}< 0.Nên:\dfrac{3}{14}>0>-\dfrac{6}{14}.Vậy:\dfrac{3}{14}>-\dfrac{6}{14}\\ e,\dfrac{7}{-12}=\dfrac{7.3}{-12.3}=\dfrac{21}{-36};\dfrac{11}{-18}=\dfrac{11.2}{-18.2}=\dfrac{22}{-36}\\ Vì:\dfrac{21}{-36}>\dfrac{22}{-36}.Nên:\dfrac{7}{-12}>\dfrac{11}{-18}\)
\(f,-\dfrac{4}{7}< -\dfrac{1}{2};-\dfrac{4}{10}>\dfrac{-1}{2}.Nên:-\dfrac{4}{7}< -\dfrac{1}{2}< -\dfrac{4}{10}.Vậy:-\dfrac{4}{7}< -\dfrac{4}{10}\\ g,-\dfrac{8}{15}< -\dfrac{1}{2};\dfrac{5}{-24}>-\dfrac{1}{2}.Nên:-\dfrac{8}{15}< -\dfrac{1}{2}< \dfrac{5}{-24}.Vậy:-\dfrac{8}{15}< \dfrac{5}{-24}\\ h,\dfrac{69}{-230}=\dfrac{69:23}{-230:23}=\dfrac{3}{-10};\dfrac{-39}{143}=\dfrac{-39:13}{143:13}=\dfrac{-3}{11}\\ Vì:\dfrac{-3}{10}< -\dfrac{3}{11}.Vậy:\dfrac{69}{-230}< \dfrac{-39}{143}\\ i,\dfrac{7}{41}=1-\dfrac{34}{41};\dfrac{13}{47}=1-\dfrac{34}{47}\\ Vì:\dfrac{34}{41}>\dfrac{34}{47}.Nên:1-\dfrac{34}{41}< 1-\dfrac{34}{47}.Vậy:\dfrac{7}{41}< \dfrac{13}{47}\)

Các phân số trên đều có dạng: \(\dfrac{k}{k+n+2}\)
Chúng tối giản khi \(k\) và \(k+n+2\) nguyên tố cùng nhau
\(\Rightarrow k\) và \(k+n+2-k\) nguyên tố cùng nhau
\(\Rightarrow k\) và \(n+2\) nguyên tố cùng nhau
\(\Rightarrow n+2\) nguyên tố cùng nhau với 1;2;3;...;2002
Mà n nhỏ nhất \(\Rightarrow n+2=2003\) (do 2003 là số nguyên tố nên nó nguyên tố cùng nhau với mọi số nguyên)
\(\Rightarrow n=2001\)

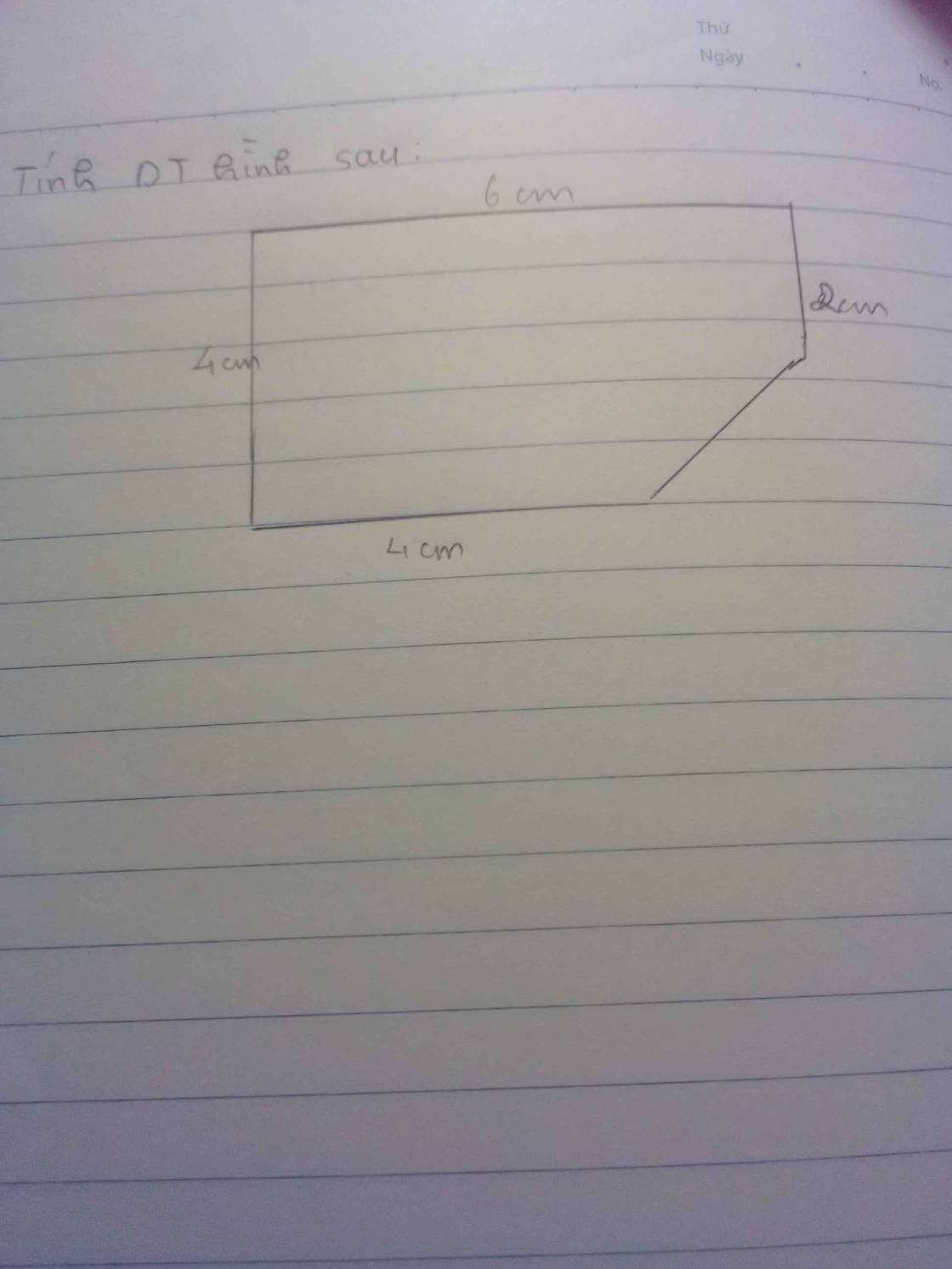
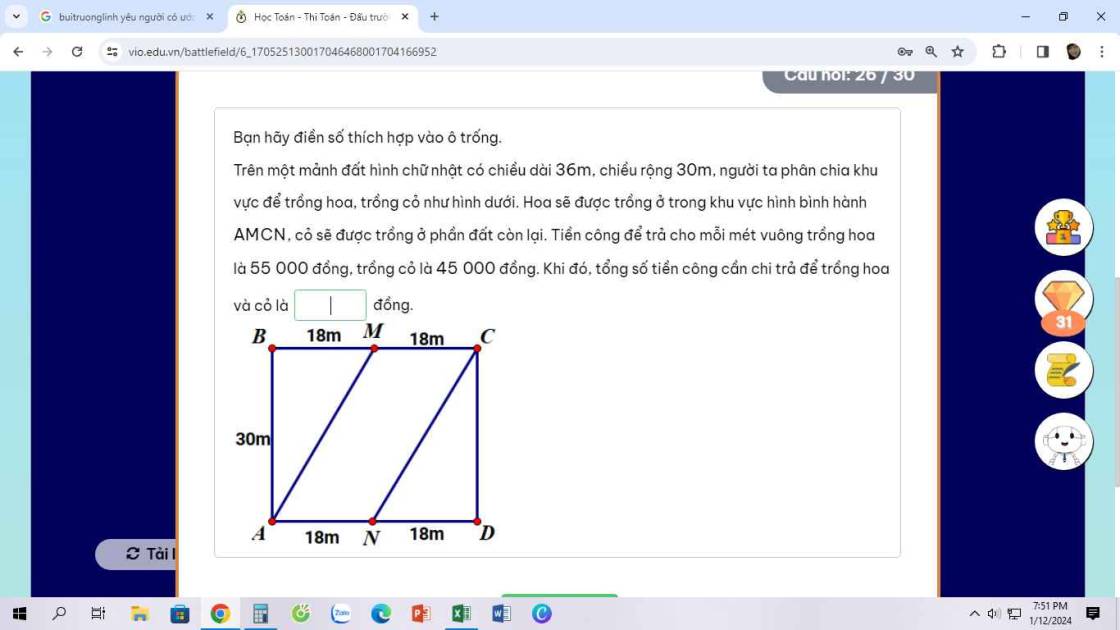
Diện tích mảnh đất là:
\(30\times\left(18+18\right)=1080\left(m^2\right)\)
Diện tích trồng hoa là:
\(30\times18=540\left(m^2\right)\)
Diện tích trồng cỏ là:
\(1080-540=540\left(m^2\right)\)
Tổng tiền cần chi trả là:
\(55000\times540+45000\times540=54000000\) (đồng)
Giải
Diện tích mảnh đất là:
30x(18+18)=1080(m vuông)
Diện tích trồng hoa là:
30x18=540(m vuông)
Diện tích trồng cỏ là:1080-540=540(m vuông)
Tổng số tiền cần chị trả là:
55000x540+45000x540=54000000(đồng)
Chúc bạn học tốt!

Bài 1:
a; 24 ⋮ \(x\); 30 ⋮ \(x\); 48 \(⋮\) \(x\) và \(x\) lớn nhất.
vì 24 \(⋮\) \(x\); 30 ⋮ \(x\); 48 ⋮ \(x\) ⇒ \(x\) \(\in\) ƯC(24; 30; 48)
Vì \(x\) là lớn nhât nên \(x\) \(\in\) ƯCLN(24; 30; 48)
24 = 22.33; 30 = 2.3.5; 48 = 24.3
ƯCLN(24; 30; 48) = 2.3 = 6
⇒ \(x\) = 6
Vậy \(x\) = 6
b; 120 ⋮ \(x\); 180 ⋮ \(x\); 30 ⋮ \(x\)
⇒ \(x\) \(\in\) ƯC(120; 180; 390)
120 = 23.3.5; 180 = 22.32.5; 390 = 2.3.5.13
ƯC(120; 180; 390) = 2.3.5 = 30
⇒ \(x\in\) Ư(30) = {1; 2; 3; 5; 6; 10;15; 30}
Vì 5 ≤ \(x\) ≤ 15 nên \(x\) \(\in\) {5; 6; 10; 15}



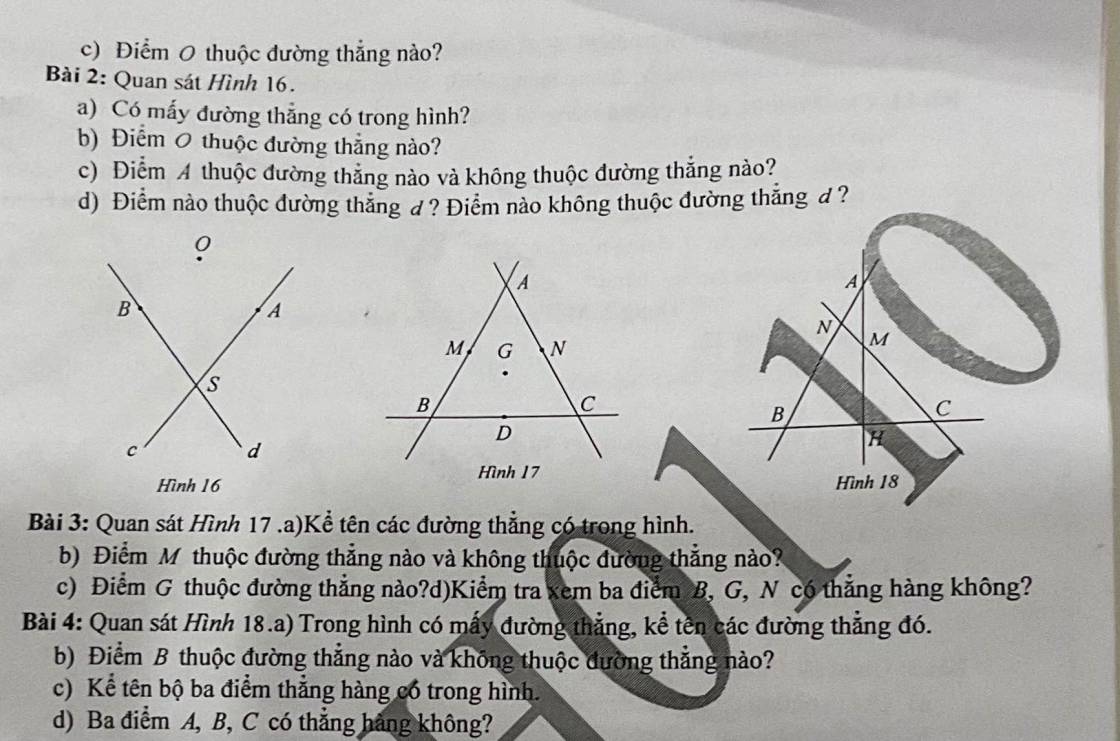
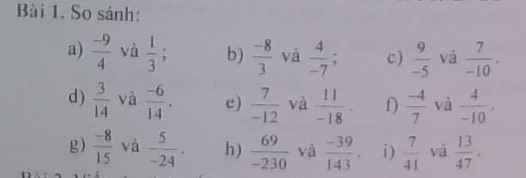
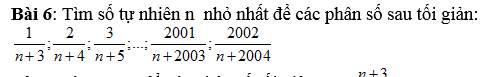

\(E=\dfrac{10n+6}{2n-3}=\dfrac{10n-15+21}{2n-3}=5+\dfrac{21}{2n-3}\)
Để E có giá trị lớn nhất thì \(\dfrac{21}{2n-3}\) max
=>2n-3=1
=>2n=4
=>n=2
Để E min thì 2n-3=-1
=>2n=2
=>n=1