
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 4:
a; \(\dfrac{1}{4}\) - \(\dfrac{1}{5}\) = \(\dfrac{5}{20}\) - \(\dfrac{4}{20}\) = \(\dfrac{1}{20}\)
b; \(\dfrac{3}{5}\) - \(\dfrac{-1}{2}\) = \(\dfrac{6}{10}\) + \(\dfrac{5}{10}\) = \(\dfrac{11}{10}\)
c; \(\dfrac{3}{5}\) - \(\dfrac{-1}{3}\) = \(\dfrac{9}{15}\) + \(\dfrac{5}{15}\) = \(\dfrac{14}{15}\)
d; \(\dfrac{-5}{7}\) - \(\dfrac{1}{3}\)= \(\dfrac{-15}{21}\) - \(\dfrac{7}{21}\)= \(\dfrac{-22}{21}\)
Bài 5
a; 1 + \(\dfrac{3}{4}\) = \(\dfrac{4}{4}\) + \(\dfrac{3}{4}\) = \(\dfrac{7}{4}\) b; 1 - \(\dfrac{1}{2}\) = \(\dfrac{2}{2}\) - \(\dfrac{1}{2}\) = \(\dfrac{1}{2}\)
c; \(\dfrac{1}{5}\) - 2 = \(\dfrac{1}{5}\) - \(\dfrac{10}{5}\) = \(\dfrac{-9}{5}\) d; -5 - \(\dfrac{1}{6}\) = \(\dfrac{-30}{6}\) - \(\dfrac{1}{6}\) = \(\dfrac{-31}{6}\)
e; - 3 - \(\dfrac{2}{7}\)= \(\dfrac{-21}{7}\) - \(\dfrac{2}{7}\)= \(\dfrac{-23}{7}\) f; - 3 + \(\dfrac{2}{5}\) = \(\dfrac{-15}{5}\) + \(\dfrac{2}{5}\)= - \(\dfrac{13}{5}\)
g; - 3 - \(\dfrac{2}{3}\) = \(\dfrac{-9}{3}\) - \(\dfrac{2}{3}\) = \(\dfrac{-11}{3}\) h; - 4 - \(\dfrac{-5}{7}\) = \(\dfrac{-28}{7}\)+ \(\dfrac{5}{7}\) = - \(\dfrac{23}{7}\)

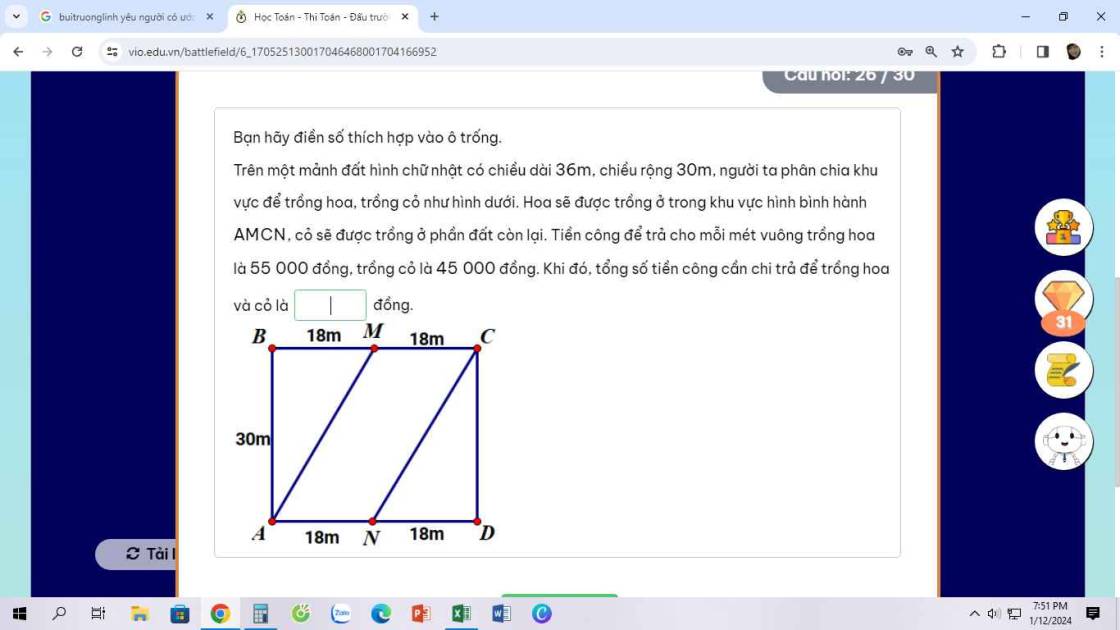
Diện tích mảnh đất là:
\(30\times\left(18+18\right)=1080\left(m^2\right)\)
Diện tích trồng hoa là:
\(30\times18=540\left(m^2\right)\)
Diện tích trồng cỏ là:
\(1080-540=540\left(m^2\right)\)
Tổng tiền cần chi trả là:
\(55000\times540+45000\times540=54000000\) (đồng)
Giải
Diện tích mảnh đất là:
30x(18+18)=1080(m vuông)
Diện tích trồng hoa là:
30x18=540(m vuông)
Diện tích trồng cỏ là:1080-540=540(m vuông)
Tổng số tiền cần chị trả là:
55000x540+45000x540=54000000(đồng)
Chúc bạn học tốt!

Bài 5:
a. Gọi $d=ƯCLN(n-2, n+1)$
$\Rightarrow n-2\vdots d; n+1\vdots d$
$\Rightarrow (n+1)-(n-2)\vdots d$
$\Rightarrow 3\vdots d\Rightarrow d\in \left\{1; 3\right\}$
Để ps tối giản thì $n-2\not\vdots 3$
$\Leftrightarrow n\neq 3k+2$ với $k$ là số tự nhiên bất kỳ.
b.
Gọi $d=ƯCLN(n+5, n-2)$
$\Rightarrow n+5\vdots d; n-2\vdots d$
$\Rightarrow (n+5)-(n-2)\vdots d$
$\Rightarrow 7\vdots d$
$\Rightarrow d\in \left\{1; 7\right\}$
Để ps tối giản thì $n-2\not\vdots 7$
$\Rightarrow n\neq 7k+2$ với $k$ là số tự nhiên bất kỳ.

Có quá nhiều bài, thứ nhất em đăng tách ra, thứ hai chụp gần cận cho rõ, thứ ba em chỉ đăng bài cần giúp

\(a,MSC:180\\ Có:-5=\dfrac{-5.180}{180}=\dfrac{-900}{180};\dfrac{17}{-20}=\dfrac{17.\left(-9\right)}{\left(-9\right).\left(-20\right)}=\dfrac{-153}{180};\dfrac{-16}{9}=\dfrac{-16.20}{9.20}=\dfrac{-320}{180}\\ ---\\ b.MSC:75\\ Có:\dfrac{13}{-15}=\dfrac{13.\left(-5\right)}{\left(-15\right).\left(-5\right)}=\dfrac{-65}{75};\dfrac{-18}{25}=\dfrac{-18.3}{25.3}=\dfrac{-54}{75};-3=\dfrac{-3.75}{75}=\dfrac{-225}{75}\)

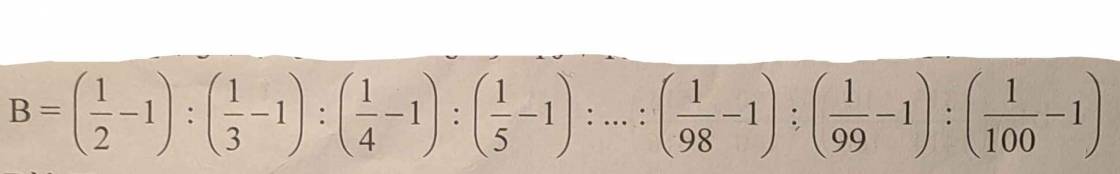 Giúp em với ạ
Giúp em với ạ

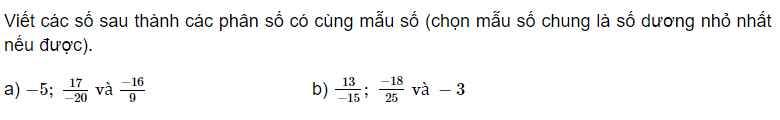
\(B=\left(\dfrac{1}{2}-1\right)\div\left(\dfrac{1}{3}-1\right)\div\left(\dfrac{1}{4}-1\right)\div...\div\left(\dfrac{1}{100}-1\right)\)
\(=\dfrac{-1}{2}\div\dfrac{-2}{3}\div\dfrac{-3}{4}\div...\div\dfrac{-99}{100}\)
\(=-\dfrac{1}{2}\times\dfrac{3}{2}\times\dfrac{4}{3}\times...\times\dfrac{100}{99}=-\dfrac{100}{2\times2}=-25\)