
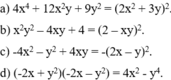
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

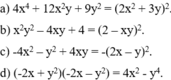



\(P=\left(x-y\right)^2+\left(x+y\right)^2-2\left(x+y\right)\left(x-y\right)-4x^2=\left(x-y-x-y\right)^2-\left(2x\right)^2=\left(-2y\right)^2-\left(2x\right)^2\)
\(=\left(2y-2x\right)\left(2y+2x\right)=2\left(y-x\right)2\left(y+x\right)=4\left(x+y\right)\left(y-x\right)\)
\(x^3-x^2y+3x-3y=x^2\left(x-y\right)+3\left(x-y\right)=\left(x-y\right)\left(x^2+3\right)\)
\(x^3-2x^2-4xy^2+x=x\left(x^2-2x+1-4y^2\right)=x\left[\left(x-1\right)^2-\left(2y\right)^2\right]=x\left(x+2y-1\right)\left(x-2y-1\right)\)
\(\left(x+2\right)\left(x+3\right)\left(x+4\right)\left(x+5\right)-8=\left(x^2+7x+10\right)\left(x^2+7x+12\right)-8\)
Đặt \(x^2+7x+10=t\), ta có:
\(t\left(t+2\right)-8=t^2+2t-8=t^2-2t+4t-8=t\left(t-2\right)+4\left(t-2\right)=\left(t-2\right)\left(t+4\right)\)
\(=\left(x^2+7x+10+4\right)\left(x^2+7x+10-2\right)=\left(x^2+7x+14\right)\left(x^2+7x-8\right)\)

Bài1: Phân tích các đa thức sau thành nhân tử
a)36-4x2+4xy-y2
\(=6^2-\left(4x^2-4xy+y^2\right)\)
\(=6^2-\left(2x-y\right)^2\)
\(=\left(6+2x-y\right)\left(6-2x+y\right)\)
b)2x4+3x2-5
\(=2x^4-2x^2+5x^2-5\)
\(=2x^2\left(x^2-1\right)+5\left(x^2-1\right)\)
\(=\left(2x^2+5\right)\left(x^2-1\right)\)
\(=\left(2x^2+5\right)\left(x-1\right)\left(x+1\right)\)
B1:a)\(36-4x^2+4xy-y^2=36-\left(4x^2-4xy+y^2\right)=6^2-\left(2x-y\right)^2\)
\(=\left(6-2x+y\right)\left(6+2x-y\right)\)
c)\(a^3-ab^2+a^2+b^2-2ab=a\left(a^2-b^2\right)+\left(a-b\right)^2\)\(=a\left(a-b\right)\left(a+b\right)+\left(a-b\right)^2=\left(a-b\right)\left(a^2+ab+a-b\right)\)
d)\(x^2-\left(a^2+b^2\right)x+a^2b^2=x^2-a^2x-b^2x+a^2b^2\)\(=x\left(x-a^2\right)-b^2\left(x-a^2\right)=\left(x-a^2\right)\left(x-b^2\right)\)
e)\(x\left(x-y\right)+x^2-y^2=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)\(=\left(x-y\right)\left(x+x+y\right)=\left(x-y\right)\left(2x+y\right)\)

\(x^2-2x-4y^2-4y\)
\(=\left(x^2-4y^2\right)-\left(2x+4y\right)\)
\(=\left(x-2y\right)\left(x+2y\right)-2\left(x+2y\right)\)
\(=\left(x+2y\right)\left(x-2y-2\right)\)
\begin{array}{l} a){\left( {ab - 1} \right)^2} + {\left( {a + b} \right)^2}\\ = {a^2}{b^2} - 2ab + 1 + {a^2} + 2ab + {b^2}\\ = {a^2}{b^2} + 1 + {a^2} + {b^2}\\ = {a^2}\left( {{b^2} + 1} \right) + \left( {{b^2} + 1} \right)\\ = \left( {{a^2} + 1} \right)\left( {{b^2} + 1} \right)\\ c){x^3} - 4{x^2} + 12x - 27\\ = {x^3} - 27 + \left( { - 4{x^2} + 12x} \right)\\ = \left( {x - 3} \right)\left( {{x^2} + 3x + 9} \right) - 4x\left( {x - 3} \right)\\ = \left( {x - 3} \right)\left( {{x^2} + 3x + 9 - 4x} \right)\\ = \left( {x - 3} \right)\left( {{x^2} - x + 9} \right)\\ b){x^3} + 2{x^2} + 2x + 1\\ = {x^3} + 2{x^2} + x + x + 1\\ = x\left( {{x^2} + 2x + 1} \right) + \left( {x + 1} \right)\\ = x{\left( {x + 1} \right)^2} + \left( {x + 1} \right)\\ = \left( {x + 1} \right)\left( {x\left( {x + 1} \right) + 1} \right)\\ = \left( {x + 1} \right)\left( {{x^2} + x + 1} \right)\\ d){x^4} - 2{x^3} + 2x - 1\\ = {x^4} - 2{x^3} + {x^2} - {x^2} + 2x - 1\\ = {x^2}\left( {{x^2} - 2x + 1} \right) - \left( {{x^2} - 2x + 1} \right)\\ = \left( {{x^2} - 2x + 1} \right)\left( {{x^2} - 1} \right)\\ = {\left( {x - 1} \right)^2}\left( {x - 1} \right)\left( {x + 1} \right)\\ = {\left( {x - 1} \right)^3}\left( {x + 1} \right)\\ e){x^4} + 2{x^3} + 2{x^2} + 2x + 1\\ = {x^4} + 2{x^3} + {x^2} + {x^2} + 2x + 1\\ = {x^2}\left( {{x^2} + 2x + 1} \right) + \left( {{x^2} + 2x + 1} \right)\\ = \left( {{x^2} + 2x + 1} \right)\left( {{x^2} + 1} \right)\\ = {\left( {x + 1} \right)^2}\left( {{x^2} + 1} \right) \end{array} |

Câu 1:
a/ (-5x3)(2x2+3x-5)
=-10x5-15x4+25x3
b/(2x-1)x
=2x2-x
c/(x-y)(3x2+4xy)
=3x3+4x2y-3x2y-4xy2
=3x3 +x2y-4xy2
Câu 2:
a/ x3-2x2+x
=x(x2-2x+1)
=x(x-1)2
b/x2-x-12
=x2 +3x-4x-12
=(x2 +3x)+(-4x-12)
=x(x+3)-4(x+3)
=(x+3)(x-4)
c/ 2x-6
=2(x-3)
e/ x2+4x+4-y2
=(x2+4x+4)-y2
=(x+2)2-y2
=(x+2-y)(x+2+y)
d/ x2-2xy+y2-16
=(x2-2xy+y2)-16
=(x-y)2-16
=(x-y-4)(x-y+4)
Câu 3:
a: \(=\dfrac{5xy-4+3xy+4}{2x^2y^3}=\dfrac{8xy}{2x^2y^3}=\dfrac{4}{xy^2}\)
b: \(=\dfrac{y-12}{6\left(y-6\right)}+\dfrac{6}{y\left(y-6\right)}\)
\(=\dfrac{y^2-12y+36}{6y\left(y-6\right)}=\dfrac{y-6}{6y}\)
c: \(=\dfrac{3x+1-2x+3}{x+y}=\dfrac{x+4}{x+y}\)
d: \(=\dfrac{4x+7+5x+7}{9}=\dfrac{9x+14}{9}\)
e: \(=\dfrac{5\left(x+2\right)}{2\left(2x-1\right)}\cdot\dfrac{-2\left(x-2\right)}{x+2}=\dfrac{-5\left(x-2\right)}{2x-1}\)

a,\(-4x^2+4x-1\)
\(\Leftrightarrow\left(-2x-1\right)^2\)
b,\(\left(2x+1\right)^2-4\left(x-1\right)^2\)
\(\Rightarrow\left[2x+1-2\left(x-1\right)\right].\left[2x+1+2\left(x-1\right)\right]\)
\(\Rightarrow\left(2x+1-2x+2\right)\left(2x+1+2x-2\right)\)
\(\Rightarrow3\left(4x-1\right)\)
c,\(\left(2x-y\right)^2-4x^2+12x-9\)
\(\Leftrightarrow\left(2x+y\right)^2-\left(4x^2-12x+9\right)\)
\(\Leftrightarrow\left(2x+y\right)^2-\left(2x-3\right)^2\)
\(\Leftrightarrow\left(2x+y-2x+3\right)\left(2x+y+2x-3\right)\)
\(\Rightarrow\left(y+3\right)\left(4x+y-3\right)\)
d,\(\left(x+1\right)^2-4\left(x+1\right)y^2+4y^4\)
\(\Leftrightarrow\left(x+1\right)^2-2\left(x+1\right)2y^2+2^2y^4\)
\(\Leftrightarrow\left(x+1\right)^2-2\left(x+1\right)2y^2+4\left(y^2\right)^2\)
\(\Leftrightarrow\left(x+1\right)^2-2\left(x+1\right)-2y^2+\left(2y^2\right)^2\)
\(\Leftrightarrow\left(x+1-2y^2\right)^2\)

Bài 1:
a) 25x2 - 10xy + y2 = (5x - y)2
b) 81x2 - 64y2 = (9x)2 - (8y)2 = (9x - 8y)(9x + 8y)
c) 8x3 + 36x2y + 54xy2 + 27y3
= 8x3 + 27y3 + 36x2y + 54xy2
= (2x + 3y)(4x2 - 6xy + 9y2) + 18xy(2x + 3y)
= (2x + 3y)(4x2 - 6xy + 18xy + 9y2)
= (2x + 3y)(4x2 + 12xy + 9y2)
= (2x + 3y)(2x + 3y)2 = (2x + 3y)3
c) (a2 + b2 - 5)2 - 4(ab + 2)2 = (a2 + b2 - 5)2 - 22(ab + 2)2
= (a2 + b2 - 5)2 - (2ab + 4)2
= (a2 + b2 - 5 - 2ab - 4)(a2 + b2 - 5 + 2ab + 4)
= (a2 - 2ab + b2 - 9)(a2 + 2ab + b2 - 1)
= \(\left [ (a - b)^{2} - 3^{2} \right ]\)\(\left [ (a + b)^{2} - 1\right ]\)
= (a - b - 3)(a - b + 3)(a + b - 1)(a + b + 1)
pn đăng mỗi lần vài bài thôi chứ đăng nhìn ngán lắm
Bài 2:
a) 2x3 + 3x2 + 2x + 3
= 2x3 + 2x + 3x2 + 3
= 2x(x2 + 1) + 3(x2 + 1)
= (x2 + 1)(2x + 3)
b)x3z + x2yz - x2z2 - xyz2
= xz(x2 + xy - xz - yz)
= \(xz\left [ x(x + y) - z(x + y) \right ]\)
= xz(x + y)(x - z)
c) x2y + xy2 - x - y
= xy(x + y) - (x + y)
= (x + y)(xy - 1)
d) 8xy3 - 5xyz - 24y2 + 15z
= 8xy3 - 24y2 - 5xyz + 15z
= 8y2(xy - 3) - 5z(xy - 3)
= (xy - 3)(8y2 - 5z)
e) x3 + y(1 - 3x2) + x(3y2 - 1) - y3
= x3 - y3 + y - 3x2y + 3xy2 - x
= (x - y)(x2 + xy + y2) - 3xy(x - y) - (x - y)
= (x - y)(x2 + xy + y2 - 3xy - 1)
= (x - y)(x2 - 2xy + y2 - 1)
= \((x - y)\left [ (x - y)^{2} - 1 \right ]\)
= (x - y)(x - y - 1)(x - y + 1)
câu f tương tự