Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A.
Đặt u = x 2 - 2 x , ta có y = f u ⇒ y ' = 2 x - 2 f ' u = 2 x - 2 f ' x 2 - 2 x .
Do đó, phương trình y ' = 0 ⇔ [ 2 x - 2 = 0 x 2 - 2 x = - 2 x 2 - 2 x = - 1 x 2 - 2 x = 0 ⇔ [ x - 1 3 = 0 x 2 - 2 x + 2 = 0 x 2 - 2 x = 0 ⇔ [ x = 0 x = 1 x = 2 .
Vậy hàm số đã chốc 3 điểm cực trị là x = 0; x= 1; x = 2.

Đáp án B
Phương pháp: Đạo hàm của hàm hợp : ![]()
Tìm số nghiệm của phương trình y’ = f’(x2 – 2x) = 0
Cách giải:
![]()
![]()
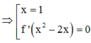
Vì f(x) liên tục trên R và có đúng ba điểm cực trị là –2; –1; 0 nên f’(x) đổi dấu tại đúng ba điểm –2; –1; 0 và f’(–2) = f’(–1) = f(0) = 0
Giải các phương trình:
![]() : vô nghiệm
: vô nghiệm
![]()
![]()

Như vậy, y’ = 0 có 3 nghiệm x = 0;1;2 và y’ đều đổi dấu tại 3 điểm này. Do đó, hàm số y = f(x2 – 2x) có 3 điểm cực trị

Đáp án là C
f ' x = 0 ⇔ x x - 1 2 x + 1 = 0 ⇔ x = 0 x = 1 x = - 1
Nhận thấy x=1 là nghiệm bội chẵn nên f’(x) không đổi dấu qua x=1 do đó x=1 không phải là điểm cực trị của hàm số.
Nhận thấy x=0; x=-1 là các nghiệm bội lẻ nên f’(x) sẽ đổi dấu qua x=0; x=-1.
Vậy hàm số có 2 điểm cực trị
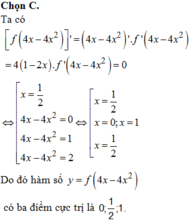

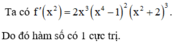



Chọn đáp án D
Ta thấy y’ đổi dấu 3 lần => Hàm số đã cho có 3 điểm cực trị.
Lưu ý: Có thể giải thích đạo hàm của hàm số đã cho không xác định tại theo 2 cách như sau:
(Đọc bài đọc thêm “Đạo hàm một bên”, SGK Đại số và Giải tích 11, NXB GDVN).
Lưu ý: Ta có thể giải nhanh bài toán trên dựa vào nhận xét sau: “Số điểm cực trị của hàm số y = |f(x)| bằng tổng số điểm cực trị của hàm số y = f(x) và số nghiệm (không trùng với các điểm cực trị) của phương trình f(x) = 0''.
Mặt khác phương trình f(x) = 0 có nghiệm duy nhất x = 2 (không trùng với các điểm cực trị nêu trên).