Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hai vật có li độ ngang nhau khi hình chiếu vị trí của chúng trên trục hoành trùng nhau.
+ Dựa vào giản đồ vecto ta có thể thấy được khoảng thời gian 2 lần liên tiếp chúng trùng nhau là T 2


\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Đáp án A
+ Biểu diễn hai vị trí tương ứng trên đường tròn, ta dễ dàng xác định được △ φ = 0 , 5 π
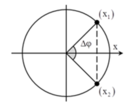

Đáp án A
Giả sử tại thời điểm ban đầu hai chất điểm đều có tọa độ là x = 6 cm và ngược chiều nhau
φ 1 = 53 0 φ 2 = - 45 0
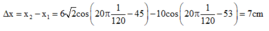

Phương trình khoảng cách giữa 2 vật :
\(\Delta x=10\cos\left(\pi t\right)cm\)
Tại thời điểm 2 vật đi ngang qua nhau tức là cùng li độ.
Thời gian ngắn nhất chúng cách nhau thỏa mãn tại thời điểm t1, chúng cùng đi qua VTCB (tốc độ cực đại)
Thời gian \(\Delta x\)từ 0 đến 5cm xác định trên đường tròn
\(t=\frac{T}{12}=\frac{1}{6}s\)
Chọn A

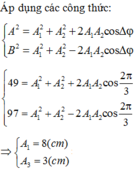
Chọn B