
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

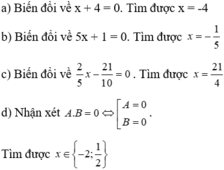

a) đặt \(\left(x^2+x\right)\)là \(y\)
ta có: \(3y^2-7y+4\)\(=0\)
<=>\(\left(3y-4\right)\left(y-1\right)=0\)
còn lại bạn tự xử nhé

a) 7x - 35 = 0
<=> 7x = 0 + 35
<=> 7x = 35
<=> x = 5
b) 4x - x - 18 = 0
<=> 3x - 18 = 0
<=> 3x = 0 + 18
<=> 3x = 18
<=> x = 5
c) x - 6 = 8 - x
<=> x - 6 + x = 8
<=> 2x - 6 = 8
<=> 2x = 8 + 6
<=> 2x = 14
<=> x = 7
d) 48 - 5x = 39 - 2x
<=> 48 - 5x + 2x = 39
<=> 48 - 3x = 39
<=> -3x = 39 - 48
<=> -3x = -9
<=> x = 3

Nhìn sơ qua thì thấy bài 3, b thay -2 vào x rồi giải bình thường tìm m
Bài 2:
a) \(x+x^2=0\)
\(\Leftrightarrow x\left(x+1\right)=0\)
\(\Leftrightarrow\hept{\begin{cases}x=0\\x+1=0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\x=0-1\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x=0\\x=-1\end{cases}}\)
b) \(0x-3=0\)
\(\Leftrightarrow0x=3\)
\(\Rightarrow vonghiem\)
c) \(3y=0\)
\(\Leftrightarrow y=0\)

a) 2x^2 + 3 = 2x(x + 4) - 7
<=> 2x^2 + 3 = 2x^2 + 8x - 7
<=> 2x^2 - 2x^2 - 8x = - 7 - 3
<=> -8x = -10
<=> x = -10/-8 = 5/4
b) 4x^2 - 12x + 5 = 0
<=> 4x^2 - 2x - 10x + 5 = 0
<=> 2x(2x - 1) - 5(2x - 1) = 0
<=> (2x - 5)(2x - 1) = 0
<=> 2x - 5 = 0 hoặc 2x - 1 = 0
<=> x = 5/2 hoặc x = 1/2
c) |5 - 2x| = 1 - x
<=> \(\hept{\begin{cases}5-2x\text{ nếu }5-2x\ge0\Leftrightarrow x\ge\frac{5}{2}\\-\left(5-2x\right)\text{ nếu }5-2x< 0\Leftrightarrow x< \frac{5}{2}\end{cases}}\)
+) nếu x >= 5/2, ta có:
5 - 2x = 1 - x
<=> -2x + 1 = 1 - 5
<=> -x = -4
<=> x = 4 (tm)
+) nếu x < 5/2, ta có:
-(5 - 2x) = 1 - x
<=> -5 + 2x = 1 - x
<=> 2x + 1 = 1 + 5
<=> 3x = 6
<=> x = 2 (ktm)
d) \(\frac{2}{x-1}=\frac{\left(2x-1\right)\left(2x+1\right)}{x^3-1}-\frac{2x+3}{x^2+x+1}\) ; ĐKXĐ: x # 1
<=> \(\frac{2}{x-1}=\frac{\left(2x-1\right)\left(2x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{2x+3}{x^2+x+1}\)
<=> \(\frac{2\left(x^2+x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}=\frac{\left(2x-1\right)\left(2x+1\right)}{\left(x-1\right)\left(x^2+x+1\right)}-\frac{\left(2x+3\right)\left(x-1\right)}{\left(x-1\right)\left(x^2+x+1\right)}\)
<=> 2(x^2 + x + 1) = (2x - 1)(2x + 1) - (2x + 3)(x - 1)
<=> 2x^2 + 2x + 2 = 2x^2 - x + 2
<=> 2x^2 - 2x^2 + 2x - x = 2 - 2
<=> x = 0
mạn phép vô đây để kiếm câu trả lời
\(2x^2+3=2x\left(x+4\right)-7\)
\(< =>2x^2+3=2x.x+4.2x-7\)
\(< =>2x^2+3=2x^2+8x-7\)
\(< =>2x^2+3-2x^2=8x-7\)
\(< =>\left(2x^2-2x^2\right)-8x=-7-3\)
\(< =>-8x=-10< =>8x=10\)
\(< =>x=10:8=\frac{10}{8}=\frac{5}{4}\)

a, 8/x-8 + 11/x-11 = 9/x-9 + 10/ x-10
b, x/x-3 - x/x-5 = x/x-4 - x/x-6
c, 4/x^2-3x+2 - 3/2x^2-6x+1 +1 = 0
d, 1/x-1 + 2/ x-2 + 3/x-3 = 6/x-6
e, 2/2x+1 - 3/2x-1 = 4/4x^2-1
f, 2x/x+1 + 18/x^2+2x-3 = 2x-5 /x+3
g, 1/x-1 + 2x^2 -5/x^3 -1 = 4/ x^2 +x+1

a) ĐKXĐ : \(x\ne-2;x\ne5\)
\(\frac{7}{x+2}=\frac{3}{x-5}\)
<=> 3(x + 2) = 7(x - 5)
<=> 3x + 6 = 7x - 35
<=> 4x = 41
<=>x = 41/4 (tm)
Vậy x = 41/4 là ngiệm phương trình
b) ĐKXĐ \(x\ne\pm3\)
\(\frac{2x-1}{x+3}=\frac{2x}{x-3}\)
<=> \(\frac{\left(2x-1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}=\frac{2x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}\)
<=> (2x - 1)(x - 3) = 2x(x + 3)
<=> 2x2 - 7x + 3 = 2x2 + 6x
<=> 13x = 3
<=> x = 3/13 (tm)
Vậy x = 3/13 là nghiệm phương trình
c) ĐKXĐ : \(x\ne-7;x\ne1,5\)
Khi đó \(\frac{3x-2}{x+7}=\frac{6x+1}{2x-3}\)
<=> \(\frac{\left(3x-2\right)\left(2x-3\right)}{\left(x+7\right)\left(2x-3\right)}=\frac{\left(6x+1\right)\left(x+7\right)}{\left(x+7\right)\left(2x-3\right)}\)
<=> (3x - 2)(2x - 3) = (6x + 1)(x + 7)
<=> 6x2 - 13x + 6 = 6x2 + 43x + 7
<=> 56x = -1
<=> x = -1/56 (tm)
Vậy x = -1/56 là nghiệm phương trình
d) ĐKXĐ : \(x\ne\pm1\)
Khi đó \(\frac{2x+1}{x-1}=\frac{5\left(x-1\right)}{x+1}\)
<=> \(\frac{\left(2x+1\right)\left(x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{5\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\)
<=> (2x + 1)(x + 1) = 5(x - 1)2
<=> 2x2 + 3x + 1 = 5x2 - 10x + 5
<=> 3x2 - 13x + 4 = 0
<=> 3x2 - 12x - x + 4 = 0
<=> 3x(x - 4) - (x - 4) = 0
<=> (3x - 1)(x - 4) = 0
<=> \(\orbr{\begin{cases}3x-1=0\\x-4=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{3}\left(tm\right)\\x=4\left(tm\right)\end{cases}}\)
Vậy x \(\in\left\{\frac{1}{3};4\right\}\)là nghiệm phương trình
e) ĐKXĐ : \(x\ne1\)
Khi đó \(\frac{4x-5}{x-1}=2+\frac{x}{x-1}\)
<=> \(\frac{3x-5}{x-1}=2\)
<=> 3x - 5 = 2(x - 1)
<=> 3x - 5 = 2x - 2
<=> x = 3 (tm)
Vậy x = 3 là nghiệm phương trình
f) ĐKXĐ : \(x\ne-1\)
\(\frac{1-x}{x+1}+3=\frac{2x+3}{x+1}\)
<=> \(\frac{3x+2}{x+1}=3\)
<=> 3x + 2 = 3(x + 1)
<=> 3x + 2 = 3x + 3
<=> 0x = 1
<=> \(x\in\varnothing\)
Vậy tập nghiệm phương trình S = \(\varnothing\)
g) ĐKXĐ : \(x\ne2\)
Khi đó \(\frac{1}{x-2}+3=\frac{x-3}{2-x}\)
<=>\(\frac{x-2}{x-2}=3\)
<=> (x - 2) = 3(x - 2)
<=> x - 2 = 3x - 6
<=> -2x = -4
<=> x = 2 (loại)
Vậy tập nghiệm phương trình S = \(\varnothing\)
h) ĐKXĐ : \(x\ne7\)
Khi đó \(\frac{1}{7-x}=\frac{x-8}{x-7}-8\)
<=> \(\frac{x-7}{x-7}=8\)
<=> x - 7 = 8(x - 7)
<=> x - 7 = 8x - 56
<=> 7x = 49
<=> x = 7 (loại)
Vậy tập nghiệm phương trình S = \(\varnothing\)
i) ĐKXĐ : \(x\ne0;x\ne6\)
Ta có : \(\frac{x+6}{x}=\frac{1}{2}+\frac{15}{2\left(x-6\right)}\)
<=> \(\frac{x+6}{x}-\frac{15}{2\left(x-6\right)}=\frac{1}{2}\)
<=> \(\frac{2\left(x+6\right)\left(x-6\right)}{2x\left(x-6\right)}-\frac{15x}{2x\left(x-6\right)}=\frac{1}{2}\)
<=> \(\frac{2x^2-72-15x}{2x\left(x-6\right)}=\frac{1}{2}\)
<=> 4x2 - 144 - 30x = 2x(x - 6)
<=> 2x2 - 18x - 144 = 0
<=> x2 - 9x - 72 = 0
<=> x2 - 9x + 81/4 - 72- 81/4 = 0
<=> \(\left(x-\frac{9}{2}\right)^2-\frac{369}{4}=0\)
<=> \(\left(x-\frac{9}{2}+\sqrt{\frac{369}{4}}\right)\left(x-\frac{9}{2}-\sqrt{\frac{369}{4}}\right)=0\)
<=> \(\orbr{\begin{cases}x=\frac{9}{2}-\sqrt{\frac{369}{4}}\\x=\frac{9}{2}+\sqrt{\frac{369}{4}}\end{cases}}\)(tm)
Vậy x \(\in\left\{\frac{9}{2}-\sqrt{\frac{369}{4}};\frac{9}{2}+\sqrt{\frac{369}{4}}\right\}\)