Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

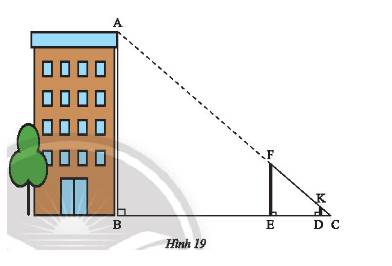
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A,F,K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất( 3 điểm F,K,C thẳng hàng).
b) ∆BC có AB // EF nên EFABEFAB = ECBCECBC => AB = EF.BCECEF.BCEC = h.abh.ab
Vậy chiều cao của bức tường là: AB = h.abh.ab.

a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, vuông góc với mặt đất sau đó di chuyển cọc 2 sao cho 3 điểm A, F, K thẳng hàng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
Sử dụng hệ quả của định lý Ta – let để tính chiều cao AB.
b) Ta có:
\(\left. \begin{array}{l}AB \bot BC\\DK \bot BC\end{array} \right\} \Rightarrow AB\parallel DK\)
Xét tam giác ABC với \(AB\parallel DK\) ta có:
\(\frac{{DK}}{{AB}} = \frac{{CD}}{{CB}}\) (Hệ quả của định lý Thales)
\( \Rightarrow AB = \frac{{DK.CB}}{{CD}} = \frac{{h.a}}{b}\).

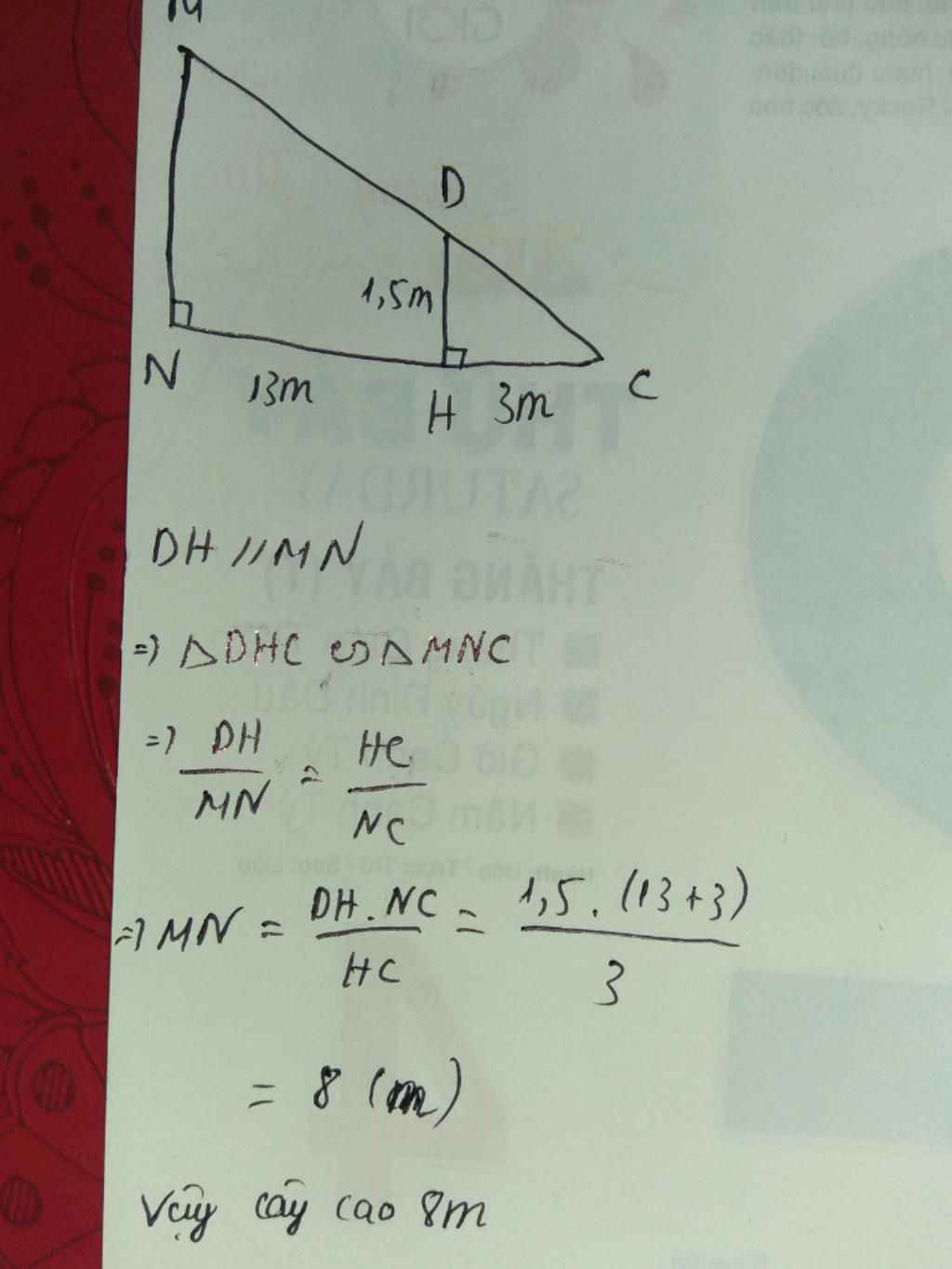
Vì \(\left\{ \begin{array}{l}KD \bot BC\\AB \bot BC\end{array} \right. \Rightarrow KD//AB\).
Xét tam giác \(CAB\) có \(KD//AB \Rightarrow \frac{{KD}}{{AB}} = \frac{{DC}}{{BC}}\) (hệ quả của định lí Thales).
\( \Rightarrow \frac{1}{{AB}} = \frac{{1,2}}{{24}} \Rightarrow AB = \frac{{24.1}}{{1,2}} = 20m\)
Vậy chiều cao \(AB\) của tòa nhà là 20m.

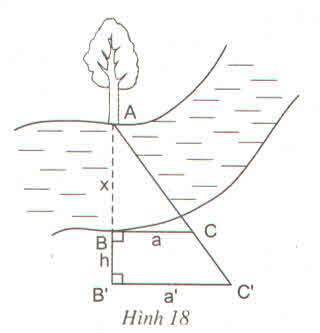
Ta có:
ABAB′ABAB′ = BCBC′BCBC′ mà AB' = x + h nên
xx+hxx+h = aa′aa′ <=> a'x = ax + ah
<=> a'x - ax = ah
<=> x(a' - a) = ah
x= aha′−aaha′−a
Vậy khoảng cách AB bằng aha′−a
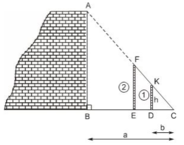
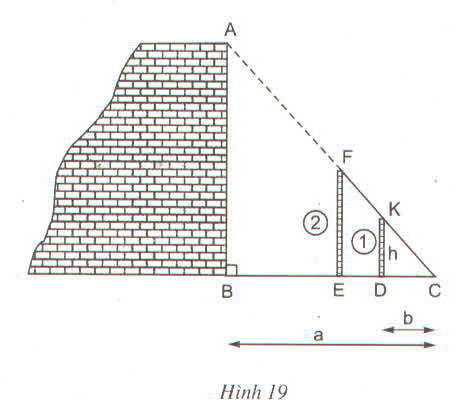
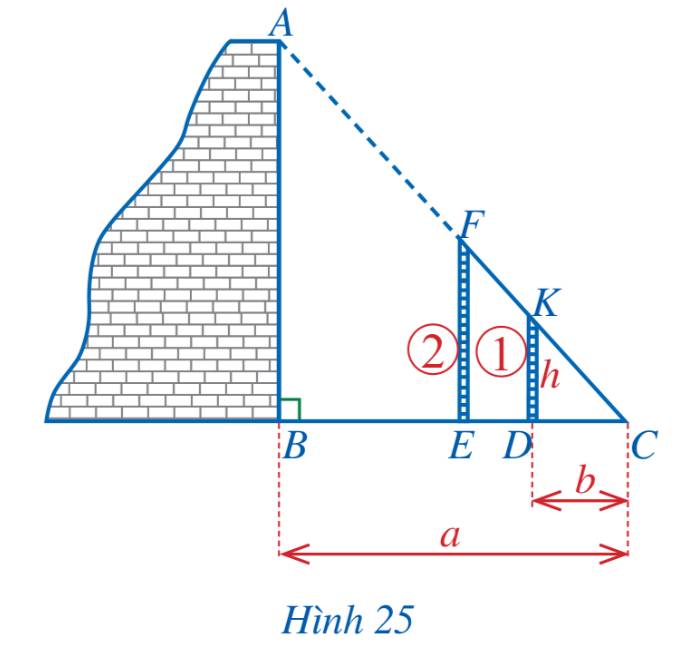

a) Cách tiến hành:
- Đặt hai cọc thẳng đứng, di chuyển cọc 2 sao cho 3 điểm A, F, K nằm trên đường thẳng.
- Dùng sợi dây căng thẳng qua 2 điểm F và K để xác định điểm C trên mặt đất (3 điểm F, K, C thẳng hàng).
b) ΔABC có AB // KD (D ∈ BC, K ∈ AC)
Vậy chiều cao bức tường là