

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




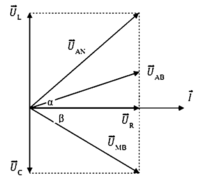
\(Z_{LR}=100\Omega\)
\(Z_{RC}=\frac{100}{\sqrt{3}}\)
Nhận xét: Do \(R^2=Z_LZ_C\) nên uAN vuông pha với uMB
\(\Rightarrow\left(\frac{u_{AN}}{U_{0AN}}\right)^2+\left(\frac{u_{MB}}{U_{0MB}}\right)^2=1\)
\(\Rightarrow\left(\frac{80\sqrt{3}}{I_0.100}\right)^2+\left(\frac{60}{I_0.\frac{100}{\sqrt{3}}}\right)^2=1\)
\(\Rightarrow I_0=\sqrt{3}\)
\(\Rightarrow U_0=I_0.Z=\sqrt{3}\sqrt{50^2+\left(50\sqrt{3}-\frac{50\sqrt{3}}{3}\right)^2}=50\sqrt{7}V\)

Chọn đáp án B
Ta có: Z L R . Z C R = 2 ⇒ Điện áp hai đầu AN và MB vuông pha nhau
Mặt khác: Z A N = 3 Z M B ⇒ U A N = 3 U M B
⇒ u A N 2 U A N 2 + u M B 2 U M B 2 = 1 ⇔ 80 3 6 U M B 2 + 60 2 U M B 2 = 1 ⇔ U M B = 50 2 V ⇒ U A N = 50 6 V
Lại có: cos φ A N 2 + cos φ M B 2 = 1
⇔ U R 2 50 2 2 + U R 2 50 6 2 = 1 ⇔ U R = 25 6 V

Đáp án B
Phương pháp: Sử dụng giản đồ Frenen
Cách giải:
Ta có
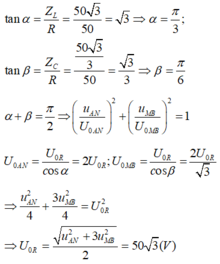
Độ lệch pha giữa u và i là φ:
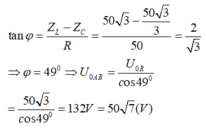

Chọn đáp án C
Khi ω = ω 1 thì điện áp hai đầu đoạn mạch AN và MB vuông pha nhau Z L R Z C R = 1 → Z L Z C = R 2
→ ta chuẩn hóa R = 1 Z L = X → Z C = 1 X
Kết hợp với U M B = 2 U A N ⇔ R 2 + Z C 2 = 4 R 2 + Z L 2 ⇔ 1 + 1 X 2 = 4 + 4 X 2
→ X = 0 , 5
Khi ω = ω 1 = 100 π 2 r a d / s (ta giả sử rằng ω 2 = n ω 1 ) thì điện áp trên hai đầu cuộn cảm đạt cực đại
Z ' C 2 = Z ' L Z ' C − R 2 2 ⇔ 1 n X 2 = 1 − 1 2 = 1 2 ⇔ n = 2 2
→ Vậy ω 1 = 50 π r a d / s

Chọn đáp án C
Khi ω = ω 1 thì điện áp hai đầu đoạn mạch AN và MB vuông pha nhau :
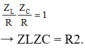
→
ta chuẩn hóa 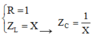
Kết hợp với
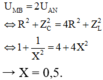
Khi ![]() (ta giả sử rằng
(ta giả sử rằng ![]() ) thì điện áp trên hai đầu cuộn cảm đạt cực đại
) thì điện áp trên hai đầu cuộn cảm đạt cực đại
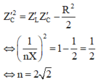
→ Vậy ω 1 = 50 π r a d / s .