Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Giả sử đa giác đã cho có n cạnh thì chu vi đa giác đó là S n = u 1 + u 2 + . . + u n với u 1 , u 2 , . . , u n lần lượt là số đo các cạnh của đa giác 0 < u 1 < u 2 < . . . < u n = 44 c m
Suy ra S n = u 1 + u n . n 2
![]()
Do n ∈ ℕ nên u 1 + 44 là ước nguyên dương của 316
Mà 316 = 2 7 . 79 nên u 1 = 44 ∈ 2 ; 4 ; 79 ; 158 ; 316
* Với u 1 + 44 = 2 ⇔ u 1 = - 42 < 0 (Loại).
* Với u 1 + 44 = 4 ⇔ u 1 = - 40 < 0 (Loại).
* Với u 1 + 44 = 79 ⇔ u 1 = 35 ⇔ n = 4
* Với u 1 + 44 = 158 ⇔ u 1 = 114 ⇔ n = 2 (Loại do số cạnh của một đa giác luôn lớn hơn 2, tức là n > 2 , n ∈ ℕ ) .
* Với u 1 + 44 = 316 ⇔ u 1 = 272 ⇔ n = 1 (Loại).
Vậy đa giác đã cho có 4 cạnh.

Đáp án B
Ta sắp xếp các cạnh giá trị u 1 ; … u n tăng dần theo cấp số cộng là 3. Khi đó ta có:
S n = 158 u n = 44 ⇔ u 1 + 44 . n 2 = 158 u 1 + 3 n − 1 = 44 ⇔ u 1 = 47 − 3 n 47 − 3 n + 44 . n = 316 *
* ⇔ 3 n 2 − 91 n + 316 = 0 ⇔ n = 4 T M n = 79 3 L

Đáp án B.
Các cạnh từ bé đến lơn tạo thành một cấp số cộng có u 1 = 25 và công sai d = 3 . Gọi số cạnh của đa giác là n ≥ 3
Chu vi là
S n = u 1 + u 2 + u 3 + … + u n = n u 1 + n ( n − 1 ) 2 d
⇒ 155 = n 25 + n ( n − 1 ) 2 .3 ⇒ n = 5 n = − 62 3 ( 1 ) .
Vậy đa giác đó là ngũ giác.
Nhận xét: Độc giả có thể thử từng phương án vào để tìm kết quả.

Đáp án A
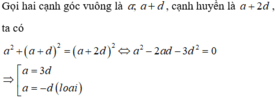
Do đó 3 cạnh của tam giác vuông cần tìm có dạng 3d ;4d ;5d, tức là một cạnh bất kì phải chia hết cho 3, hoặc chia hết cho 4, hoặc chia hết cho 5.
Trong các đáp án, chỉ có số 81 thỏa mãn chia hết cho 3.






Đáp án B
Gọi số cạnh đa giác là n ta có
44 n − 3 1 + 2 + ... + n − 1 = 158 ⇔ 44 n − 3 n n − 1 2 = 158
⇔ 3 n 2 − 91 n + 316 = 0 ⇒ n = 4