

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án B
+ Áp dụng công thức
![]()
![]()
+ Vận tốc dài: ![]()
+ Gia tốc hướng tâm:
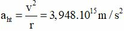

Chọn đáp án D
Tần số của chuyển động: f = 1/12 Hz
Tốc độ góc của chuyển động: ![]() = 0,523 rad / s
= 0,523 rad / s
Gia tốc hướng tâm: ![]()

Số vòng vật quay được trong 1 phút=60s là \(\dfrac{5}{60}=\dfrac{1}{12}\) vòng.
\(\Rightarrow f=\dfrac{1}{12}\Rightarrow T=12s\)
Tốc độ góc của người đó: \(\omega=\dfrac{2\pi}{T}=\dfrac{2\pi}{12}=\dfrac{\pi}{6}rad\)/s
Gia tốc hướng tâm: \(a_{ht}=r\cdot\omega^2=3\cdot\left(\dfrac{\pi}{6}\right)^2=0,8225\) m/s2.

Chọn đáp án C
+ Tốc độ góc: 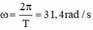
+ Tốc độ dài: ![]()
+ Gia tốc hướng tâm: ![]()

<Phàn trình bày là ở bạn mình chỉ vt công thức rùi tính kết quả thui nha>
Bài 1:
a,\(\omega=\dfrac{v}{r}=\dfrac{10}{20}=0,5\left(\dfrac{rad}{s}\right)\)
\(T=\dfrac{2\pi}{\omega}=\dfrac{2\sqrt{10}}{0,5}=4\sqrt{10}\left(s\right)\)
\(f=\dfrac{1}{T}=\dfrac{1}{4\sqrt{10}}\left(Hz\right)\)
b, \(a_{ht}=\dfrac{v^2}{r}=\dfrac{10^2}{20}=5\left(\dfrac{m}{s^2}\right)\)
c,\(s=f\cdot t\cdot2\pi r=\dfrac{1}{4\sqrt{10}}\cdot30\cdot2\cdot\sqrt{10}\cdot20=300\left(m\right)\)
<ko hiểu chỗ nào có thể liên hệ với mình nha>
Bài 1: Còn tính góc quay của ca bin trong thời gian 30 s thì làm sao ạ.

Ta có:
+ Chu kì quay của bánh xe: T=2100=0,02sT=2100=0,02s
+ Tần số: f=1T=50Hzf=1T=50Hz
+ Tốc độ góc: ω=2πT=2π0,02=100π(rad/s)ω=2πT=2π0,02=100π(rad/s)
+ Tốc độ dài của một điểm trên vành bánh xe: v=ωR=100π.0,6≈188,5m/s

Đổi 30 cm =0,3 m; 1 phút =60s
a,\(T=\dfrac{1}{f}=\dfrac{1}{\dfrac{N}{t}}=\dfrac{1}{\dfrac{60}{60}}=1\left(s\right)\)
\(\omega=\dfrac{2\pi}{T}=2\pi\left(\dfrac{rad}{s}\right)\)
b,\(v=\dfrac{2\pi}{T}\cdot r=0,6\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}=\dfrac{v^2}{r}=\dfrac{\left(0,6\pi\right)^2}{0,3}=1,2\pi^2\left(\dfrac{m}{s^2}\right)\)
c, Đổi 10 cm =0,1m
Khoảng cách từ tâm đến điểm được xét =0,3-0,1=0,2(m)
<Rùi tính tiếp>
\(v'=\dfrac{2\pi}{T}r'=0,4\pi\left(\dfrac{m}{s}\right)\)
\(a_{ht}'=\dfrac{v'^2}{r'}=\dfrac{\left(0,4\pi\right)^2}{0,3}=\dfrac{8}{15}\pi^2\left(\dfrac{m}{s^2}\right)\)