Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


nên \(V_{A'B'C'D'}=\dfrac{1}{27}V_{ABCD}=\dfrac{\sqrt{2}}{324}a^2\)

S M H G N A O D C
Ta có \(\begin{cases}BC\perp SA\\BC\perp AB\end{cases}\)\(\Rightarrow BC\perp\left(SAB\right)\)\(\Rightarrow BC\perp AM\) (vì \(AM\subset\left(SAB\right)\left(1\right)\)
Mặt khác \(SC\perp\alpha\Rightarrow SA\perp AM\) (vì \(AM\subset\alpha\)) (2)
Từ (1) và (2) suy ra \(AM\perp\left(SBC\right)\Rightarrow AM\perp MG\) (vì \(MG\subset\left(SBC\right)\))
\(\Rightarrow\Delta AMG\) vuông tại M, tương tự ta cũng có tam giác ANG vuông tại N \(\Rightarrow\) tâm H đường tròn đáy của (H) là trung điểm AG, có bán kính \(R=\frac{AG}{2}\)
Xét tam giác vuông SAC tại A có \(AG=\frac{SA.AC}{SC}=\frac{\sqrt{6}}{3}a\Rightarrow R=\frac{\sqrt{6}}{6}a\)
Vì OH là đường cao (H)\(\Rightarrow OH\perp\alpha\Rightarrow OH\)//\(SC\Rightarrow O\) là giao điểm hai đường chéo AC, BD
\(\Rightarrow OH=\frac{1}{2}CG\).
Xét tam giác vuoongSAC có AG là đường cao, nên \(CG=\frac{AC^2}{SC}=\frac{2}{\sqrt{3}}a\Rightarrow OH=\frac{\sqrt{3}}{3}a\)
Vậy thể tích hình nón là \(V_{\left(H\right)}=\frac{1}{3}\pi.R^2.OH=\frac{\sqrt{3}}{54}\pi a^3\)
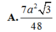
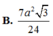
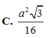
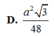

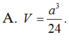
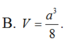
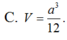
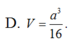
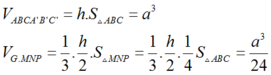
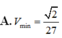
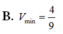
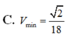
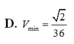

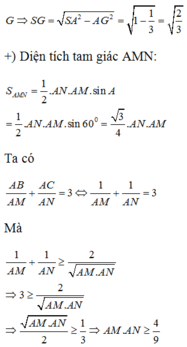
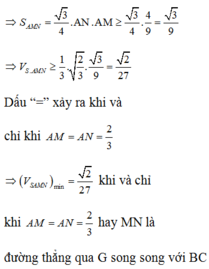
Chọn D
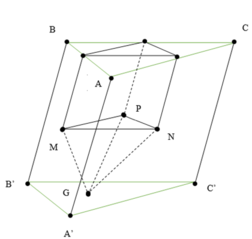
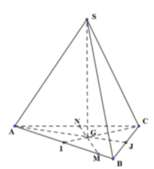
Tứ diện đều ABCD ⇒ A G 1 ⊥ B C D
Ta có ngay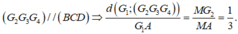
Cạnh C G 1 = B C 3 = 3 ⇒ G 1 A = A C 2 - G 1 C 2 = 6 ⇒ d G 1 ; G 2 G 3 G 4 = 6 3
Lại có G 2 G 3 M N = A G 2 A M = 2 3 ⇒ G 2 G 3 = 2 3 M N = 1 3 B D = 1
Tương tự G₃G₄=1, G₄G₂=1 ⇒ ∆ G 2 G 3 G 3 là tam giác đều có cạnh bằng 1