Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B.
Ta có: S A ⊥ S B S A ⊥ S C ⇒ S A ⊥ ( S B C )
Vì vậy áp dụng công thức cho trường hợp khối chóp có cạnh bên vuông góc đáy có:
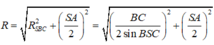
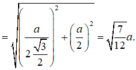

A B C D H K S
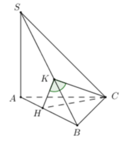
Hạ \(SH\perp BC\Rightarrow\left(SBC\right)\perp\left(ABC\right)\)
\(\Rightarrow SH\perp BC;SH=SB.\sin\widehat{SBC}=a\sqrt{3}\)
Diện tích : \(S_{ABC}=\frac{12}{\boxtimes}BA.BC=6a^2\)
Thể tích : \(V_{s.ABC}=\frac{1}{3}S_{ABC}.SH=2a^3\sqrt{3}\)
Hạ \(HD\perp AC\left(D\in AC\right),HK\perp SD\left(K\in SD\right)\)
\(\Rightarrow HK\perp\left(SAC\right)\Rightarrow HK=d\left(H,\left(SAC\right)\right)\)
\(BH=SB.\cos\widehat{SBC}=3a\Rightarrow BC=4HC\)
\(\Rightarrow d\left(B,\left(SAC\right)\right)=4d\left(H,SAC\right)\)
Ta có : \(AC=\sqrt{BA^2+BC^2}=5a;HC=BC-BH=a\)
\(\Rightarrow HD=BA.\frac{HC}{AC}=\frac{3a}{5}\)
\(HK=\frac{SH.HS}{\sqrt{SH^2+HD^2}}=\frac{3a\sqrt{7}}{14}\)
Vậy \(d\left(B,\left(SAC\right)\right)=4HK=\frac{6a\sqrt{7}}{7}\)

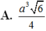

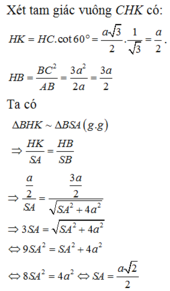
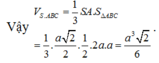






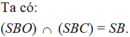
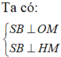
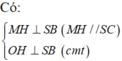
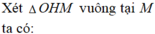
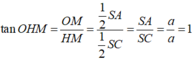
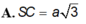
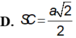



Mình không thạo vẽ hình trên này nên bạn tự vẽ hình nhé.
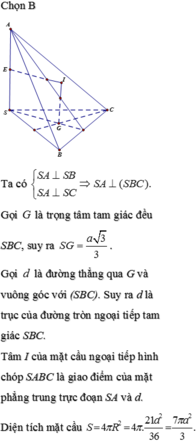
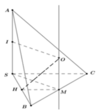
Gọi K là hình chiếu vuông góc của S trên BC.
Giả sử \(\overrightarrow{CK}=x\overrightarrow{CB}\left(0< x< 1\right)\)
Đặt \(SC=ka\Rightarrow\left\{{}\begin{matrix}BC=a\sqrt{k^2+4}\\AC=a\sqrt{k^2+8}\end{matrix}\right.\)
Ta có: \(\dfrac{1}{SK^2}=\dfrac{1}{SB^2}+\dfrac{1}{SC^2}=\dfrac{1}{\left(2a\right)^2}+\dfrac{1}{\left(ka\right)^2}\)
\(\Rightarrow SK=\dfrac{2ka}{\sqrt{k^2+4}}\)
Ta có:
\(\left(\left(SBC\right);\left(ABC\right)\right)=45^0\)
\(\Rightarrow\left(AB;SK\right)=45^0\)
\(\Leftrightarrow\dfrac{\overrightarrow{AB}.\overrightarrow{SK}}{AB.SK}=cos45^0\Leftrightarrow\dfrac{\overrightarrow{AB}.\overrightarrow{SK}}{AB.SK}=\dfrac{\sqrt{2}}{2}\)
Lại có:
\(\overrightarrow{AB}.\overrightarrow{SK}=\left(\overrightarrow{SB}-\overrightarrow{SA}\right).\left[x\overrightarrow{SB}+\left(1-x\right)\overrightarrow{SC}\right]\)
\(=xSB^2-x\overrightarrow{SA}.\overrightarrow{SB}+\left(x-1\right).\overrightarrow{SC}.\overrightarrow{SA}\)
\(=x.4a^2-x.4a^2.\dfrac{1}{2}+\left(x-1\right).\dfrac{4a^2+k^2a^2-a^2\left(k^2+8\right)}{2}\)
\(=2xa^2+\left(x-1\right).\left(-2a^2\right)=2a^2\)
\(\Rightarrow\dfrac{\sqrt{2}}{2}=\dfrac{2a^2}{2a.\dfrac{2ka}{\sqrt{k^2+4}}}\Leftrightarrow k=2\)
Do đó:
\(\left\{{}\begin{matrix}SC=2a\\BC=2a\sqrt{2}\\AC=2a\sqrt{3}\end{matrix}\right.\)
Ta có:
\(R=\sqrt{R_{SAB}^2+R_{ABC}^2-\dfrac{AB^2}{4}}\)
\(=\sqrt{\left(\dfrac{2a\sqrt{3}}{3}\right)^2+\left(a\sqrt{3}\right)^2-\dfrac{\left(2a\right)^2}{4}}=\dfrac{a\sqrt{30}}{3}\)
\(\Rightarrow S=4\pi R^2=4\pi.\dfrac{10}{3}a^2=\dfrac{40}{3}\pi a^2\)
dạ em nhờ các anh chị, các bạn giải giúp mình bài toán này với ạ!