Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B M C N D P Q
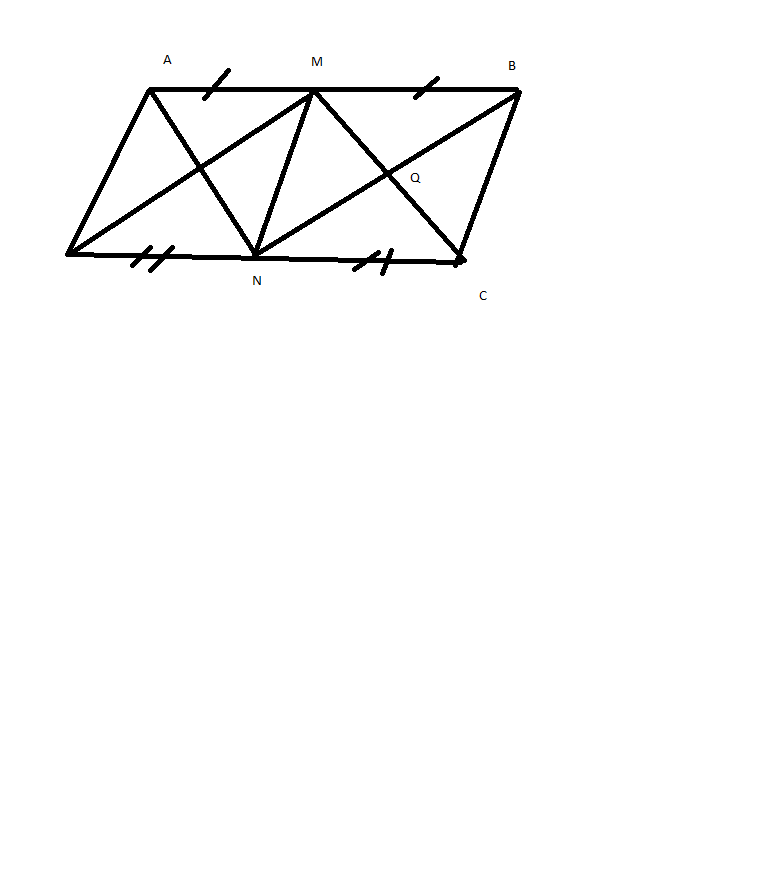
a) Do AB = 2a, AD = A nên AB = 2AD.
Lại có ABCD là hình bình hành nên AB = CD. Vậy thì \(DN=\frac{CD}{2}=\frac{AB}{2}=AD\)
Xét tam giác ADN có DA = DN nên ADN là tam giác cân tại D.
Do tam giác ADN cân tại D nên \(\widehat{DAN}=\widehat{DNA}\)
Do AB//DC nên \(\widehat{BAN}=\widehat{DNA}\) (Hai góc so le trong)
Vậy nên \(\widehat{DAN}=\widehat{BAN}\) hay AN là phân giác góc \(\widehat{BAD}\)
b) Ta có \(MB=\frac{1}{2}AB;DN=\frac{1}{2}DC\Rightarrow\) MB song song và bằng ND.
Xét tứ giác MDNB có MB song song và bằng ND hay MDNB là hình bình hành.
Vậy thì MD // NB
c) Tương tự câu b, ta chứng minh được AMCN là hình bình hành hay AN // MC
Xét tứ giác MPNQ có MP//QN và MQ//PN nên MPNQ là hình bình hành.
Xét tứ giác AMND có AM song song và bằng ND hay AMND là hình bình hành.
Lại có AD = AM nên AMND là hình thoi. Suy ra AN vuông góc DM hay \(\widehat{MPN}=90^o\) .
Xét hình bình hành MPNQ có \(\widehat{MPN}=90^o\) nên MPNQ là hình chữ nhật.

https://drive.google.com/file/d/1F7_WT5J17JGrHKXFz0mns6lWgsUhJcNq/view

a) Ta có :
P là trung điểm AB
Q là trung điểm AC
⇒⇒ PQ là đường trung bình tam giác ABC
Xét tứ giác BPQC , ta có :
PQ//BC( do PQ là đường trung bình tam giác ABC)
⇒⇒BPQC là hình thang (dấu hiệu nhận biết hình thang)
b)Ta có :
Q là trung điểm PE
Q là trung điểm AC
⇒⇒ Q là trung điểm hai đường chéo của tứ giác AECP
Suy ra tứ giác AECP là hình bình hành
a) Ta có :
P là trung điểm AB
Q là trung điểm AC
⇒ PQ là đường trung bình tam giác ABC
Xét tứ giác BPQC , ta có :
PQ//BC( do PQ là đường trung bình tam giác ABC)
⇒BPQC là hình thang (dấu hiệu nhận biết hình thang)

a) Vì ABCD là hình bình hành nên
AB=CD=2a, AD=BC=a
ta có: M,N là trung điểm của AB và CD
=> DN=1/2CD=a
=> AD=DN
Vậy tam giác ADN cân tại D(đpcm)
=> DAN=DNA
b) Ta có: AB//CD => AND=MAN(So le trong)
=> DAN=MAN
=>AN là tia phân giác của góc BAD

a)xét tứ giác ADME có
CÂB =AÊM=góc ADM=900
=>ADME là hcn
b)vì MA là đg trung tuyến nên MA=MC=MB
xét tam giác CMA có
CM=MA(cmt)
CÊM=AÊM=900
EM là cạnh chung
=>...(cạnh huyền-cạnh góc vuông)
=>CE=EA
mà EA=MD(EAMD là hcn) nên CE=MD (1)
ta có MA=MC(cmt)
mà MA=ED(EAMD là hcn)
=>MC=ED (2)
xét tứ giác CMDE có CE=MD,CM=ED( 1 và 2)
=>CMED là hbh
c)
xét tam giác MDB vuông tại D có DI là trung tuyến nên MI=IB=ID
xét tứ giác MKDI có
KM=KD(K là giao điểm hai dg chéo của hcn)
KM=MI(vì MA=MB mà K và I lần lượt là trung điểm của chúng)
MI=ID(cmt)
=>KMID là thoi
mà KI là đg chéo của góc I nên KI cũng là p/g của góc I
(ck hk tốt nhé)

a, Do ABCD là hình bình hành ( gt )
=> BAD + ADC = 180 độ ( t/c hbh )
Mà BAD = 120 độ ( gt ) => ADC = 60 độ
Gọi đường phân giác của góc ADC đi qua trung điểm cạnh AB là DI
=> ADI = CDI = 30 độ
Xét tam giác ADI có : DAI + ADI + AID = 180 độ ( tổng 3 góc của 1 tam giác )
=> AID = ADI = 30 độ => Tam giác AID cân
=> AI = AD mà AI = 1/2 AB => AD = 1/2 AB hay AB = 2.AD ( đpcm )
b, CM ADF đều
Do ABCD là hbh ( gt ) => AB = CD ( t/c hbh )
=> 1/2 AB = 1/2 CD => AI = BI = DF = CF
mà AI = AD => AD = DF
=> tam giác ADF cân tại D có góc ADF = 60 độ ( cmt )
=> ADF đều
CM AFC cân :
DO tam giác ADF đều ( cmt ) => AF = DF ( t/c tg đều )
mà DF = FC ( gt ) => AF = FC => tam giác AFC cân tại F ( đpcm )
c, Ta có : AF = DF = CF ( cmt )
=> AF = 1/2 ( DF +CF ) => AF = 1/2 CD
Xét tam giác ADC có AF là trung tuyến ứng với cạnh CD
và AF = 1/2CD
=> tam giác ADC vuông tại A ( dấu hiệu nhận biết tam giác vuông )
=> AD vuông góc với AD ( Đpcm )
chép mạng :))