Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Vì I là tâm đối xứng của đồ thị C ⇒ I 2 ; 2
Gọi M x 0 ; 2 x 0 − 1 x 0 − 2 ∈ C ⇒ y ' x 0 = − 3 x 0 − 2 2 suy ra phương trình tiếp tuyến Δ là
y − y 0 = y ' x 0 x − x 0 ⇔ y − 2 x 0 − 1 x 0 − 2 = − 3 x 0 − 2 2 x − x 0 ⇔ y = − 3 x 0 − 2 2 + 2 x 0 2 − 2 x 0 + 2 x 0 − 2 2
Đường thẳng Δ cắt TCĐ tại A 2 ; y A → y A = 2 x 0 + 2 x 0 − 2 ⇒ A 2 ; 2 x 0 + 2 x 0 − 2
Đường thẳng Δ cắt TCN tại B x B ; 2 → x B = 2 x 0 − 2 ⇒ B 2 x 0 − 2 ; 2
Suy ra I A = 6 x 0 − 2 ; I B = 2 x 0 − 2 → I A . I B = 6 x 0 − 2 .2 x 0 − 2 = 12
Tam giác IAB vuông tại I ⇒ R Δ I A B = A B 2 = I A 2 + I B 2 2 ≥ 2 I A . I B 2 = 6
Dấu bằng xảy ra khi và chỉ khi I A = I B ⇔ 3 = x 0 − 2 2 ⇔ x 0 = 2 + 3 x 0 = 2 − 3
Suy ra phương trình đường thẳng Δ và gọi M, N lần lượt là giao điểm của Δ với Ox, Oy
Khi đó M 2 x 0 2 − 2 x 0 + 2 3 ; 0 , N 0 ; 2 x 0 2 − 2 x 0 + 2 3 ⇒ S Δ O M N = 1 2 O M . O N
Vậy S m a x = 14 + 8 3 ≈ 27 , 85 ∈ 27 ; 28 k h i x 0 = 2 + 3

Đáp án B
Tâm đối xứng của đồ thị (C) là giao điểm hai đường tiệm cận. (C) có tiệm cận đứng là x=-1, tiệm cận ngang là y=2 => I(-1;2)
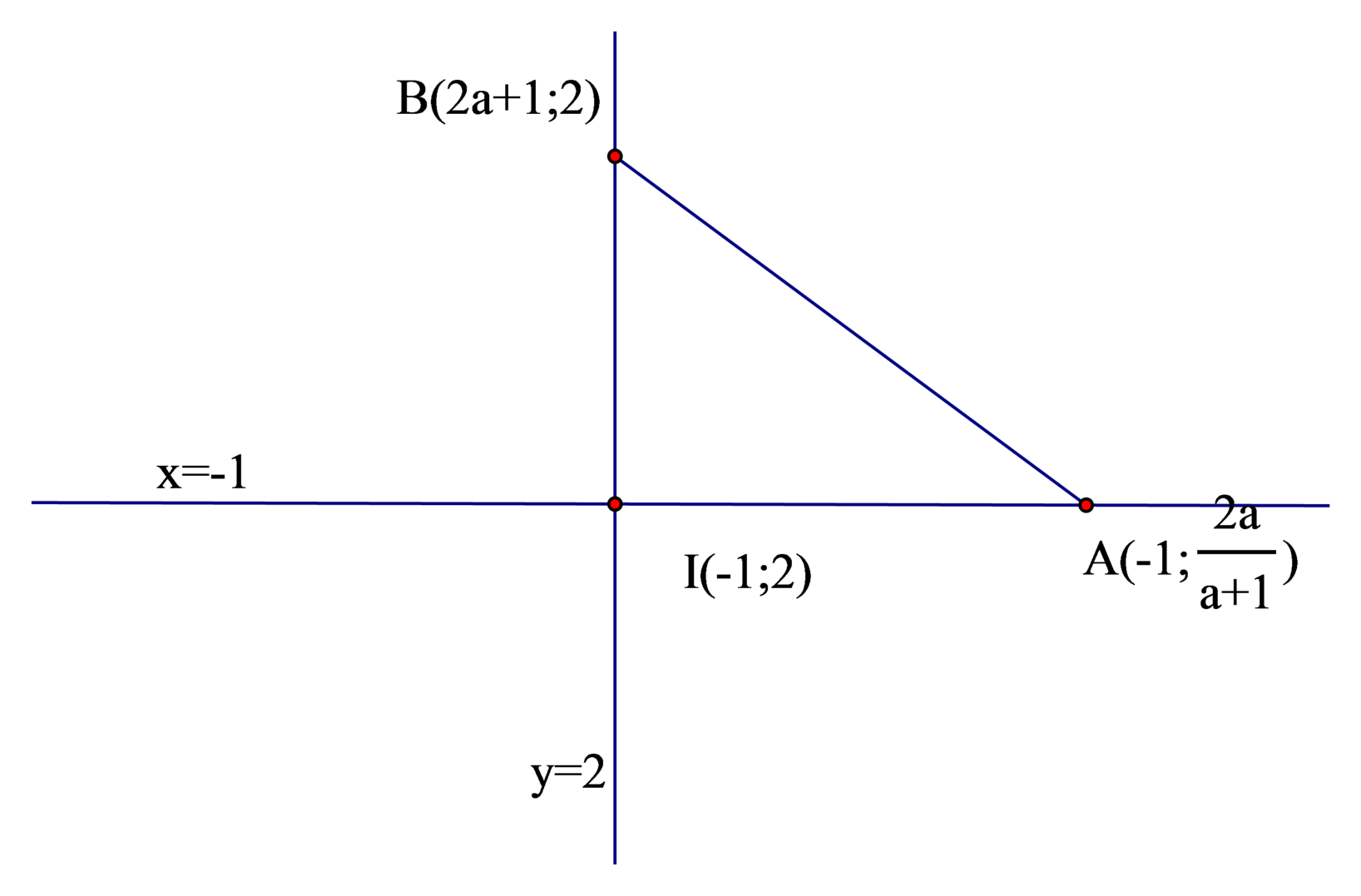
Ta có: y ' = 1 x + 1 2 ⇒ PTTT tại điểm M a ; b là y = 1 a + 1 2 x − a + 2 a + 1 a + 1 . Từ đây ta xác định được giao điểm của PTTT tại M a ; b và hai tiệm cận x = − 1 , y = 2 là A − 1 ; 2 a a + 1 , B 2 a + 1 ; 2 .
Độ dài các cạnh của Δ I A B như sau
I A = 2 a a + 1 − 2 = 2 a + 1 I B = 2 a + 1 + 1 = 2 a + 1 A B = 2 1 a + 1 2 + a + 1 2 ⇒ S I A B = 1 2 I A . I B = 2 ;
P = I A + I B + A B 2 = 1 a + 1 + a + 1 + 1 a + 1 2 + a + 1 2
Áp dụng bất đẳng thức Cosi ta có p ≥ 2 + 2 đạt được ⇔ a + 1 = 1 ⇔ a = 0 ⇒ b = 1 a = − 2 ⇒ b = 3 ⇒ a + b = 1

Ta có: M x 0 ; 2 x 0 - 3 x 0 - 2 ∈ C ; x 0 ≠ 2 ; y ' x 0 = - 1 x 0 - 2 2
Phương trình tiếp tuyến ∆ với (C) tại M:
y = - 1 x 0 - 2 x - x 0 + 2 x 0 - 3 x 0 - 2
Tọa độ giao điểm J, K của ∆ và hai tiệm cận là: J 2 ; 2 x 0 - 2 x 0 - 2 ; K 2 x 0 - 2 ; 2
Ta có
x j + x k 2 = 2 + 2 x 0 - 2 2 = x 0 = x m y j + y k 2 = 2 x 0 - 3 x 0 - 2 = y m
=> M là trung điểm JK.
Mặt khác I ( 2;2 ) và ∆ I J K vuông tại I nên đường tròn ngoại tiếp ∆ I J K có diện tích:
S = πIM 2 = π x 0 - 2 2 + 2 x 0 - 3 x 0 - 2 - 2 2 = π x 0 - 2 2 + 1 x 0 - 2 2 ≥ 2 π
Dấu “=” xảy ra khi và chỉ khi
x 0 - 2 2 = 1 x 0 - 2 2 ⇔ x 0 = 1 ⇒ M 1 ; 1 x 0 = 3 ⇒ M 3 ; 3
Đáp án A

Đáp án B
Điểm M ∈ C ⇒ M a ; 2 a + 1 a + 1 ⇒ y ' a = 1 a + 1 2
và y a = 2 a + 1 a + 1 .
Suy ra phương trình tiếp tuyến của ( C) tại M là
y = 2 a + 1 a + 1 = 1 a + 1 2 x − a ⇔ y = x a + 1 2 + 2 a 2 + 2 a + 1 a + 1 2 d .
Đường thẳng ( d ) cắt tiệm cận đứng tại
A − 1 ; 2 a a + 1 ⇒ I A = 2 a + 1 .
Đường thẳng ( d ) cắt tiệm cận ngang tại
B 2 a + 1 ; 2 ⇒ I B = 2 a + 1 .
Suy ra I A . I B = 4 và tam giác IAB vuông tại I
⇒ S Δ I A B = 1 2 . I A . I B = 2
Mà S Δ I A B = I A + I B + I C 2 x r ⇒ r m ax
khi và chỉ khi I A + I B + I C min
Ta có
I A + I B + I C = I A + I B + I A 2 + I B 2 ≥ 2 I A . I B + 2 I A . I B = 4 + 4 2 .
Dấu “=” xảy ra
⇔ 2 a + 1 = 2 a + 1 ⇔ a + 1 2 = 1 ⇔ a = 0 ⇒ b = 1 a = − 2 ⇒ b = 3 ⇒ a + b = 1.

Cho tam giác ABC đều
D thuộc AB , E thuộc AC sao cho BD = AE
CM : Khi D,E thay đổi ( di chuyển ) trên AB,AC thì đường trung tuyến DE luôn đi qua điểm cố định
Help me !!!







Đáp án C.
Ta có I 2 ; 1 .
Tiếp tuyến với C tại điểm M x 0 ; x 0 + 2 x 0 − 2 là d : y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2
Tọa độ A là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 x = 2 ⇒ y = 4 x 0 − 2 + x 0 + 2 x 0 − 2 ⇒ A 2 ; x 0 + 6 x 0 − 2 ⇒ I A → = 0 ; 8 x 0 − 2
Tọa độ B là nghiệm của hệ
y = − 4 x 0 − 2 2 x − x 0 + x 0 + 2 x 0 − 2 y = 2 ⇒ x 0 − 2 2 = − 4 x − x 0 + x 0 2 − 4 ⇒ B 2 x 0 − 2 ; 1 ⇒ I B → = 2 x 0 − 4 ; 0 Do đó C I A B = π . A B = π I A 2 + I B 2 ≥ π 2 I A . I B
Mà I A . I B = 8 x 0 − 2 . 2 x 0 − 4 = 16 ⇒ C I A B ≥ 4 π 2