Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 1: Xét trên miền [1;4]
Do \(f\left(x\right)\) đồng biến \(\Rightarrow f'\left(x\right)\ge0\)
\(x\left(1+2f\left(x\right)\right)=\left[f'\left(x\right)\right]^2\Leftrightarrow x=\frac{\left[f'\left(x\right)\right]^2}{1+2f\left(x\right)}\Leftrightarrow\frac{f'\left(x\right)}{\sqrt{1+2f\left(x\right)}}=\sqrt{x}\)
Lấy nguyên hàm 2 vế:
\(\int\frac{f'\left(x\right)dx}{\sqrt{1+2f\left(x\right)}}=\int\sqrt{x}dx\Leftrightarrow\int\left(1+2f\left(x\right)\right)^{-\frac{1}{2}}d\left(f\left(x\right)\right)=\int x^{\frac{1}{2}}dx\)
\(\Leftrightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+C\)
Do \(f\left(1\right)=\frac{3}{2}\Rightarrow\sqrt{1+2.\frac{3}{2}}=\frac{2}{3}.1\sqrt{1}+C\Rightarrow C=\frac{4}{3}\)
\(\Rightarrow\sqrt{1+2f\left(x\right)}=\frac{2}{3}x\sqrt{x}+\frac{4}{3}\)
Đến đây có thể bình phương chuyển vế tìm hàm \(f\left(x\right)\) chính xác, nhưng dài, thay luôn \(x=4\) vào ta được:
\(\sqrt{1+2f\left(4\right)}=\frac{2}{3}4.\sqrt{4}+\frac{4}{3}=\frac{20}{3}\Rightarrow f\left(4\right)=\frac{\left(\frac{20}{3}\right)^2-1}{2}=\frac{391}{18}\)
Câu 2:
Diện tích hình phẳng cần tìm là hai miền đối xứng qua Oy nên ta chỉ cần tính trên miền \(x\ge0\)
Hoành độ giao điểm: \(sinx=x-\pi\Rightarrow x=\pi\)
\(S=2\int\limits^{\pi}_0\left(sinx-x+\pi\right)dx=4+\pi^2\Rightarrow\left\{{}\begin{matrix}a=4\\b=1\end{matrix}\right.\)
\(\Rightarrow2a+b^3=9\)

Để kiểm tra một hàm F(x) có phải là một nguyên hàm của f(x) không thì ta chỉ cần kiểm tra F'(x) có bằng f(x) không?
a) \(F\left(x\right)\) là hằng số nên \(F'\left(x\right)=0\ne f\left(x\right)\)
b) \(G'\left(x\right)=2.\dfrac{1}{2}.\dfrac{1}{\cos^2x}=1+\tan^2x\)
c) \(H'\left(x\right)=\dfrac{\cos x}{1+\sin x}\)
d) \(K'\left(x\right)=-2.\dfrac{-\left(\dfrac{1}{2}.\dfrac{1}{\cos^2\dfrac{x}{2}}\right)}{\left(1+\tan\dfrac{x}{2}\right)^2}=\dfrac{\dfrac{1}{\cos^2\dfrac{x}{2}}}{\left(\dfrac{\cos\dfrac{x}{2}+\sin\dfrac{x}{2}}{\cos\dfrac{x}{2}}\right)^2}\)
\(=\dfrac{1}{\left(\cos\dfrac{x}{2}+\sin\dfrac{x}{2}\right)^2}=\dfrac{1}{1+2\cos\dfrac{x}{2}\sin\dfrac{x}{2}}\)
\(=\dfrac{1}{1+\sin x}\)
Vậy hàm số K(x) là một nguyên hàm của f(x).

7.
Thể tích:
\(V=\pi\int\limits^{\frac{\pi}{2}}_0sin^2xdx=\frac{\pi}{2}\int\limits^{\frac{\pi}{2}}_0\left(1-cos2x\right)dx=\frac{\pi}{2}\left(x-\frac{1}{2}sin2x\right)|^{\frac{\pi}{2}}_0=\frac{\pi^2}{4}\)
8.
\(z=\frac{z-17i}{5-i}\Leftrightarrow\left(5-i\right)z=z-17i\)
\(\Leftrightarrow z\left(i-4\right)=17i\Rightarrow z=\frac{17i}{i-4}=1-4i\)
Rốt cuộc câu này hỏi modun hay phần thực vậy ta?
Phần thực bằng 1
Môđun \(\left|z\right|=\sqrt{17}\)
9.
\(\left(1-3i\right)z=8+6i\Rightarrow z=\frac{8+6i}{1-3i}=-1+3i\)
\(\Rightarrow\left|z\right|=\sqrt{\left(-1\right)^2+3^2}=\sqrt{10}\)
10.
\(\left(1+i\right)^2\left(2-i\right)z=8+i+\left(1+2i\right)z\)
\(\Leftrightarrow2i\left(2-i\right)z-\left(1+2i\right)z=8+i\)
\(\Leftrightarrow\left(4i+2-1-2i\right)z=8+i\)
\(\Leftrightarrow z=\frac{8+i}{2i+1}=2-3i\)
Phần thực \(a=2\)
11.
Điểm biểu diễn số phức là điểm có tọa độ \(\left(-1;-2\right)\)
4.
\(I=\int\limits^{\frac{\pi}{2}}_{\frac{\pi}{4}}\frac{dx}{sin^2x}=-cotx|^{\frac{\pi}{2}}_{\frac{\pi}{4}}=1\)
5.
\(I=\int\limits^a_2\frac{2x-1}{1-x}dx=\int\limits^a_2\left(-2-\frac{1}{x-1}\right)dx=\left(-2x-ln\left|x-1\right|\right)|^a_2=-2a-ln\left|a-1\right|+4\)
\(\Rightarrow-2a+4-ln\left|a-1\right|=-4-ln3\Rightarrow a=4\)
6.
Phương trình hoành độ giao điểm:
\(x^3=x^5\Rightarrow\left[{}\begin{matrix}x=0\\x=1\\x=-1\end{matrix}\right.\)
Diện tích hình phẳng:
\(S=\int\limits^0_{-1}\left(x^5-x^3\right)dx+\int\limits^1_0\left(x^3-x^5\right)dx=\frac{1}{6}\)

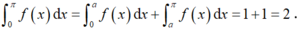
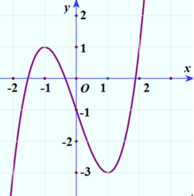



Đáp án D