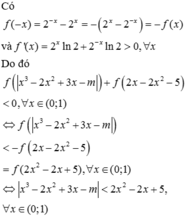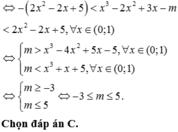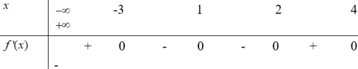Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoành độ giao điểm là nghiệm của pt
\(x^3-3mx^2+3\left(2m-1\right)x+1=2mx-4m+3\Leftrightarrow x^3-3mx^2+4mx-3x-2+4m=0\Leftrightarrow x^3-3x-2-m\left(3x^2-4x+4\right)=0\)
giải hệ pt ta có \(C_m\) luôn đi qua điểm A là nghiệm của hệ pt sau
\(\begin{cases}3x^2-4x+4=0\\x^3-3x-2=0\end{cases}\)
ta đc điều phải cm

Đặt ![]() Ta có
Ta có ![]()
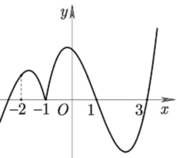
Trên đoạn [-2;3] ta có f(x) chỉ đổi dấu khi qua điểm x=1 Do vậy trước tiên cần có x=1 là nghiệm của ![]()
![]()
Điều kiện đủ:
+) Với m=−1
![]()
(đúng)
+) Với m = - 1 3

(đúng).
Vậy m = 1 , m = - 1 3 là các giá trị cần tìm.
Chọn đáp án D.

Đặt g ( x ) = m x + m 2 5 - x 2 + 2 m + 1 f ( x ) thì g(x) là hàm số liên tục trên [-2;2]
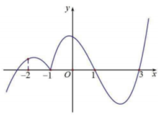
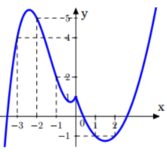
Từ đồ thị =f(x) ta thấy có nghiệm đối dấu là x=1
Do đó để bất phương trình m x + m 2 5 - x 2 + 2 m + 1 f ( x ) ≥ 0 nghiệm đúng với mọi x ∈ - 2 ; 2 thì điều kiện cần là x=1 phải là nghiệm của h ( x ) = m x + m 2 5 - x 2 + 2 m + 1
h ( 1 ) = m + 2 m 2 + 2 m + 1 ⇔ [ m = - 1 m = - 0 , 5
Do bài cần m nguyên nên ta thử lại với m=-1
h ( x ) = 5 - x 2 - x - 1 ≥ 0 , ∀ x ∈ - 2 ; 1
và h ( x ) = 5 - x 2 - x - 1 ≤ 0 , ∀ x ∈ - 2 ; 1
Dựa theo dấu y=f(x) trên đồ thị ta suy ra
g ( x ) = m x + m 2 5 - x 2 + 2 m + 1 f ( x ) ≥ 0 , ∀ x ∈ - 2 ; 2
Vậy m=-1 thỏa mãn điều kiện bài ra.
Chọn đáp án A.

Từ \(f\left(x\right)+f\left(\frac{1}{x}\right)=x^2\); lần lượt thay \(x=2\) và \(x=\frac{1}{2}\) vào, ta có:
\(f\left(2\right)+3f\left(\frac{1}{2}\right)=4\) và \(f\left(\frac{1}{2}\right)+3f\left(2\right)=\frac{1}{4}\Leftrightarrow3f\left(2\right)+f\left(\frac{1}{2}\right)=\frac{1}{4}\)
Giải hệ phương trình với 2 ẩn \(f\left(2\right)\) và \(f\left(\frac{1}{2}\right)\)
Tìm được \(f\left(2\right)=\frac{-13}{32}\)
Ta có \(f\left(x\right)+3f\left(\frac{1}{x}\right)=x^2\) (1)
Thay \(x\rightarrow\frac{1}{x}\) được \(f\left(\frac{1}{x}\right)+3f\left(x\right)=\frac{1}{x^2}\)
\(\Leftrightarrow3f\left(\frac{1}{x}\right)+9f\left(x\right)=\frac{3}{x^2}\) (2)
Lấy (2) trừ (1) theo vế : \(8f\left(x\right)=\frac{3}{x^2}-x^2\)
\(\Leftrightarrow f\left(x\right)=\frac{1}{8}\left(\frac{3}{x^2}-x^2\right)\)
Vậy f(2) = -13/32

Có ![]()
![]()
Đặt t=f(x)+m bất phương trình trở thành: ![]()
![]()
Vậy ![]()
![]()
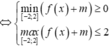
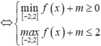
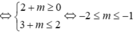
Chọn đáp án B.

Phương trình tiếp tuyến tại M0 có dạng: y = k(x – x0) + y0 (*)
Với x0 là hoành độ tiếp điểm;
Với y0 = f(x0) là tung độ tiếp điểm;
Với k = y’(x0) = f’(x0) là hệ số góc của tiếp tuyến.
Để viết được phương trình tiếp tuyến ta phải xác định được x0; y0 và k