Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a.2 + 3.
Suy ra hệ số góc a = 3/2 và được hàm số y = 3/2x + 3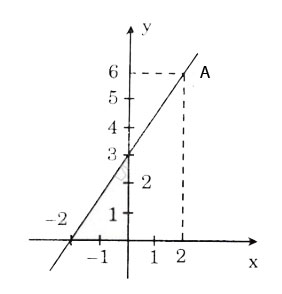
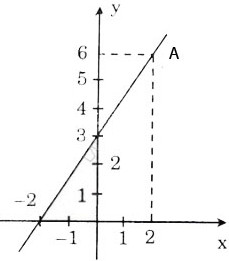
b) Hàm số đã cho là y = 3/2x + 3. Đồ thị được vẽ như hình bên.
Bài giải:
a) Vì đồ thi của hàm số đi qua điểm A(2; 6) nên ta có 6 = a . 2 + 3.
Suy ra hệ số góc a = 1, 5.
b) Hàm số đã cho là y = 1,5x + 3. Đồ thị được vẽ như hình bên.

a, Vì \(1-\sqrt{5}< 0\)nên hàm nghịch biến
b, \(x=1+\sqrt{5}x\)
\(\Leftrightarrow x-x\sqrt{5}=1\)
\(\Leftrightarrow x\left(1-\sqrt{5}\right)=1\)
\(\Leftrightarrow x=\frac{1}{1-\sqrt{5}}\)
Khi đó \(y=\left(1-\sqrt{5}\right).\frac{1}{1-\sqrt{5}}-1=1-1=0\)
b, \(y=-\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x-1=-\sqrt{5}\)
\(\Leftrightarrow\left(1-\sqrt{5}\right)x=1-\sqrt{5}\)
<=> x = 1

a) y = 1 - 5x là một hàm số bậc nhất với a = -5, b = 1. Đó là một hàm số nghịch biến vì -5 < 0.
b) y = -0,5x là một hàm bậc nhất với a \(\approx\)-0,5, b = 0. Đó là một hàm số nghịch biến vì -0,5 < 0.
c) y = \(\sqrt{ }\)2(x - 1) + \(\sqrt{ }\)3 là một hàm số bậc nhất với a = \(\sqrt{ }\)2, b = \(\sqrt{ }\)3 - \(\sqrt{ }\)2. Đó là một hàm số đồng biến vì \(\sqrt{ }\)2 > 0.
d) y = 2x2 + 3 không phải là một hàm số bậc nhất vì nó không có dạng y = ax + b, với a \(\ne\) 0.

Bài giải:
a) a = -2.
b) Ta có 7 = a . 2 + 3. Suy ra a = 2.

Đáp án C
Thay x = 1; y = 7 vào y = ax + 4, ta được:
7 = a.1 + 4
Suy ra: a = 3.