Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

E trên trục hoành nên E(x;0)
A(6;3); B(-3;6); E(x;0)
\(\overrightarrow{AB}=\left(-9;3\right);\overrightarrow{AE}=\left(x-6;-3\right)\)
Để A,B,E thẳng hàng thì \(\dfrac{x-6}{-9}=\dfrac{-3}{3}=-1\)
=>x-6=9
=>x=15
Vậy: E(15;0)
Do E thuộc trục hoành nên tọa độ có dạng \(E\left(x;0\right)\)
\(\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-9;3\right)\\\overrightarrow{AE}=\left(x-6;-3\right)\end{matrix}\right.\)
3 điểm A, B, E thẳng hàng khi:
\(\dfrac{x-6}{-9}=\dfrac{-3}{3}\Rightarrow x-6=9\)
\(\Rightarrow x=15\Rightarrow E\left(15;0\right)\)

Câu 1:
a: Vì I thuộc trục Ox nên I(x;0)
\(\overrightarrow{AI}=\left(x+1;-1\right)\)
\(\overrightarrow{AB}=\left(1;2\right)\)
Vì A,I,B thẳng hàng nên \(\dfrac{x+1}{1}=-\dfrac{1}{2}\)
=>x=-3/2
b: \(\overrightarrow{AM}=\left(m+5;2m\right)\)
Vì A,M,B thẳng hàng nên \(\dfrac{m+5}{1}=\dfrac{2m}{2}\)
=>m+5=m(vô lý)

\(\overrightarrow{AB}\left(-3;2\right)\); \(\overrightarrow{AC}\left(1;m-2\right)\).
Ba điểm A, B, C thẳng hàng khi và chỉ khi:
\(\dfrac{1}{-3}=\dfrac{m-2}{2}\Leftrightarrow-3\left(m-2\right)=2\)\(\Leftrightarrow m=\dfrac{4}{3}\).

I là trọng tâm của ΔABC
=>\(\left\{{}\begin{matrix}x_A+x_B+x_C=3\cdot x_I\\y_A+y_B+y_C=3\cdot y_I\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3+\left(-1\right)+x_C=3\cdot1=3\\-1+2+y_C=3\cdot1=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_C=3-2=1\\y_C=3-1=2\end{matrix}\right.\)
Vậy: C(1;2)
Ta có: A(3;-1); B(-1;2); C(1;2); D(x;y)
=>\(\overrightarrow{AB}=\left(-4;3\right);\overrightarrow{DC}=\left(1-x;2-y\right)\)
ABCD là hình bình hành
=>\(\overrightarrow{AB}=\overrightarrow{DC}\)
=>\(\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\)
Vậy: D(5;-1)
Tâm O của hình bình hành ABCD sẽ là trung điểm của AC
A(3;-1); C(1;2); O(x;y)
=>\(\left\{{}\begin{matrix}x=\dfrac{3+1}{2}=\dfrac{4}{2}=2\\y=\dfrac{-1+2}{2}=\dfrac{1}{2}\end{matrix}\right.\)
Áp dụng công thức trọng tâm:
\(\left\{{}\begin{matrix}x_A+x_B+x_C=3x_I\\y_A+y_B+y_C=3y_I\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_C=3x_I-\left(x_A+x_B\right)=1\\y_C=3y_I-\left(y_A+y_B\right)=2\end{matrix}\right.\)
\(\Rightarrow C\left(1;2\right)\)
Đặt tọa độ D là \(D\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AB}=\left(-4;3\right)\\\overrightarrow{DC}=\left(1-x;2-y\right)\end{matrix}\right.\)
ABCD là hình bình hành \(\Leftrightarrow\overrightarrow{AB}=\overrightarrow{DC}\)
\(\Rightarrow\left\{{}\begin{matrix}1-x=-4\\2-y=3\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=5\\y=-1\end{matrix}\right.\) \(\Rightarrow D\left(5;-1\right)\)
Tâm O hình bình hành là trung điểm đường chéo AC nên áp dụng công thức trung điểm:
\(\left\{{}\begin{matrix}x_O=\dfrac{x_A+x_C}{2}=2\\y_O=\dfrac{y_A+y_C}{2}=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow O\left(2;\dfrac{1}{2}\right)\)

Theo công thức trung điểm:
\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)
Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.
Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.
Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).
Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.
Vậy tọa độ của điểm M là M(2; 0).
Đáp án đúng là: B. M(2; 0).
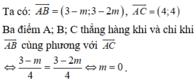
A(m-1;-1); B(2;2-2m); C(m+3;3)
\(\overrightarrow{AB}=\left(2-m+1;2-2m+1\right)\)
=>\(\overrightarrow{AB}=\left(3-m;3-2m\right)\)
\(\overrightarrow{AC}=\left(m+3-m+1;3+1\right)\)
=>\(\overrightarrow{AC}=\left(4;4\right)\)
Để A,B,C thẳng hàng thì \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\)
=>3-m=3-2m
=>m=0
\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(3-m;3-2m\right)\\\overrightarrow{AC}=\left(4;4\right)\end{matrix}\right.\)
3 điểm A;B;C thẳng hàng khi và chỉ khi \(\overrightarrow{AB}=k\overrightarrow{AC}\) với \(k\ne0\)
Hay \(\dfrac{3-m}{4}=\dfrac{3-2m}{4}\Rightarrow m=0\)