Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Answer:
Tóm tắt:
\(S=0,5mm^2=0,5.10^{-6}\Omega m\)
\(P=1,1.10^{-6}\Omega m\)
\(U=9V\)
\(I=0,25A\)
a) \(l=?\)
b) S tăng ba lần
l giảm ba lần
\(I=?\)
Giải:
Điện trở của dây dẫn Niciom:
\(R=\frac{U}{I}=\frac{9}{0,25}=36\Omega\)
Chiều dài của dây dẫn:
\(R=\frac{l}{S}\)
\(\Rightarrow l=\frac{R.S}{P}=\frac{36.0,5.10^{-6}}{1,1.10^{-6}}\approx16,36m\)
Mà: Cường độ dòng điện tỉ lệ thuận với tiết điện dây và tỉ lệ nghịch với chiều dài dây
=> I tăng sáu lần \(=0,25.6=1,5A\)
Khoảng cách ảnh AB tới thấu kính \(d_2\):
\(\dfrac{1}{f_2}=\dfrac{1}{d_2}+\dfrac{1}{d_2'}\Rightarrow d_2'=\dfrac{d_2\cdot f_2}{d_2-f_2}=\dfrac{9d_2}{d_2-9}\left(cm\right)\)
Di chuyển thấu kính lại gần màn ảnh 24 cm:
\(\Rightarrow d_2"=\dfrac{\left(d_2+24\right)\cdot f_2}{d_2+24-f_2}=\dfrac{9\left(d_2+24\right)}{d_2+15}\left(cm\right)\)
Khoảng cách giữa ảnh AB và O1 là:
\(d_2+\dfrac{9d_2}{d_2-9}=d_2+24+\dfrac{9\left(d_2+24\right)}{d_2+15}\)
\(\Rightarrow d_2^2+6d_2-216=0\Rightarrow\left[{}\begin{matrix}d_2=12cm\\d_2=-18cm\left(loại\right)\end{matrix}\right.\)
Ảnh AB cách thấu kính O1:
\(d_1'=60-12-36=12cm\)
Tiêu cự thấu kính O1:
\(\dfrac{1}{f_1}=\dfrac{1}{d_1}+\dfrac{1}{d_1'}=\dfrac{1}{12}+\dfrac{1}{12}=\dfrac{1}{6}\)
\(\Rightarrow f_1=6cm\)
Tịnh tiến AB trước thấu kính O để ảnh độ cao không phụ thuộc vào vị trí của vật.
Xảy ra\(\Leftrightarrow\)Tiêu điểm hai thấu kính trùng nhau.
\(\Leftrightarrow O_1O_2=f_1+f_2=6+9=15cm\)
Vì khi thả gói hàng, cả máy bay cả hàng đang có vận tốc nên gói hàng sẽ chuyển động theo quán tính => Gói hàng chuyển động ném ngang.
a) Thời gian để gói hàng rơi xuống đất là: 
b) Gọi v0 là tốc độ của gói hàng khi rời khỏi máy bay.
Tầm bay xa của gói hàng là: Lmax = v0t = 150.10 = 1500 m.
c. Quỹ đạo là một phần của parabol.
Câu 2 (2đ):
a) Biến trở là dụng cụ điện, dùng để thay đổi cường độ dòng điện trong mạch
b) Từ công thức \(R=p.\frac{l}{S}\)
Chiều dài dây dẫn làm biến trở là: \(l=\frac{R.S}{p}=\frac{20.0,3.10^{-6}}{0,6.10^{-6}}=10m\)
Cường độ dòng điện định mức của đèn là: \(I_{dm}=\frac{P_{dm}}{U_{dm}}=\frac{2,4}{6}=0,4A\)
Khi đèn sáng bình thường thì: \(\hept{\begin{cases}U_đ=U_{dm}=6V\\I_đ=I_{dm}=0,4A\end{cases}}\)
Vì \(ĐntR_b\)
\(\hept{\begin{cases}U_đ+U_b=U\\I_đ=I_b=0,4A\end{cases}}\)
\(\Rightarrow\hept{\begin{cases}U_b=9-6=3V\\I_b=0,4A\end{cases}}\)
Điện trở của biến trở lúc này là: \(R_b=\frac{U_b}{I_b}=\frac{3}{0,4}=7,5\Omega\)
a.P=2Vqcdqc−dnn−1b.dqc=89000N/m3a.P=2Vqcdqc−dnn−1b.dqc=89000N/m3
Giải thích các bước giải:
a.
F=Pqc−FA=Vqcdqc−Vqcdn=Vqc(dqc−dn)MAB=MqcP.12(OA−OB)=OB.F=OB.Vqc(dqc−dn)p=2.OB.Vqcdqc−dnnOB−OB=2Vqcdqc−dnn−1b.0,79.10=2.50.10−6dqc−100002−1dqc=89000N/m3
a) Vì R1 và R2 mắc nối tiếp nên chúng có cùng cường độ dòng điện chạy qua. Gọi nhiệt lượng tỏa ra ở các điện trở này tương ứng là Q1 và Q2.
Ta có: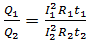 
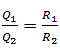
vì I1 = I2 (R1 nối tiếp với R2) và t1 = t2 suy ra 
.
b) Vì R1 và R2 mắc song song với nhau nên hiệu điện thế U giữa hai đầu của chúng là như nhau.
Ta có: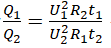 
vì U1 = U2 (R1 song song với R2 )và t1 = t2
Suy ra 
a) Vì R1 và R2 mắc nối tiếp nên chúng có cùng cường độ dòng điện chạy qua. Gọi nhiệt lượng tỏa ra ở các điện trở này tương ứng là Q1 và Q2.
Ta có: Q1Q2=I21R1t1I22R2t2Q1Q2=I12R1t1I22R2t2 vì I1 = I2 (R1 nối tiếp với R2) và t1 = t2 suy ra Q1Q2=R1R2Q1Q2=R1R2
b) Vì R1 và R2 mắc song song với nhau nên hiệu điện thế U giữa hai đầu của chúng là như nhau:
Ta có: Q1Q2=U21R2t1U22R1t2Q1Q2=U12R2t1U22R1t2 vì U1 = U2 (R1 // R2) và t1 = t2, suy ra Q1Q2=R2R1
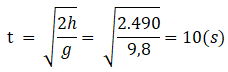
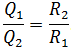
thời gian hai máy bay đi đến khi mất liên lạc là bằng nhau
=> \(\frac{100}{v1}\)+1 = 0,5 + \(\frac{400}{\frac{v2}{1,5}}\)
=> v1 = \(\frac{100.v2}{600-0,5v2}\)(biến đổi)
khoảng cách hoạt động tối đa của thiết bị định vị là 800km nên khi mất tín hiệu khoảng cách giữa 2 máy bay là 800km
\(\sqrt{\left(100+\left(v1+100\right).1\right)^2+\left(0,5v2+400\right)^2}\)=800
(thay v1 bên trên vào biểu thức bấm máy tính được v2)
\(\sqrt{\left(100+100+\frac{100v2}{600-0.5v2}\right)^2+\left(0,5v2+400\right)^2}\)=800
=> v2=591,8 km/h
thay vào cái biểu thức v1 ở trên thì tính dc v1 = 194,6 km/h