HG
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PH
1
26 tháng 11 2023
Câu 1:
\(\left\{{}\begin{matrix}y-2x< =2\\2y-x>=4\\x+y< =5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y< =2x+2\\2y>=x+4\\y< =-x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y< =2x+2\\y< =-x+5\\y>=\dfrac{1}{2}x+2\end{matrix}\right.\)
y<=2x+2
=>y-2x-2<=0
Vẽ đường thẳng y=2x+2
Khi x=0 và y=0 thì \(y-2x-2=0-0-2=-2< =0\)(đúng)
=>Miền nghiệm của BPT y<=2x+2 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y<=-x+5
=>x+y-5<=0
Khi x=0 và y=0 thì \(x+y-5=0+0-5< =0\)(đúng)
=>Miền nghiệm của BPT y<=-x+5 là nửa mặt phẳng vừa chứa biên vừa chứa điểm O(0;0)
y>=1/2x+2
=>\(-\dfrac{1}{2}x+y-2>=0\)
Khi x=0 và y=0 thì \(-\dfrac{1}{2}x+y-2=-\dfrac{1}{2}\cdot0+0-2=-2< 0\)
=>O(0;0) không thỏa mãn BPT \(-\dfrac{1}{2}x+y-2>=0\)
=>Miền nghiệm của BPT \(y>=\dfrac{1}{2}x+2\) là nửa mặt phẳng chứa biên nhưng không chứa điểm O(0;0)
Vẽ đồ thị:
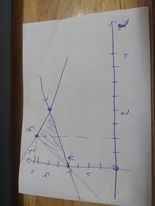
Theo hình vẽ, ta có: Miền nghiệm của hệ BPT sẽ là ΔABC, với A(0;2); B(1;4); C(2;3)
Khi x=0 và y=2 thì F=2-0=2
Khi x=1 và y=4 thì F=4-1=3
Khi x=2 và y=3 thì F=3-2=1
=>Chọn A
HG
0
3 tháng 8 2023
\(tanb-4cotb=3\)
=>\(tanb-\dfrac{4}{tanb}=3\)
=>\(tan^2b-4=3tanb\)
=>(tanb-4)(tanb+1)=0
=>tan b=-1 hoặc tan b=4
0<=b<=90
=>tan b ko thể bằng -1 được
=>tan b=4
1+tan^2b=1/cos^2b
=>1/cos^2b=17
=>cosb=1/căn 17
=>sin b=4/căn 17
\(P=\left(\dfrac{1}{\sqrt{17}}+\dfrac{4}{\sqrt{17}}\right)\cdot\sqrt{17}=5\)
NN
1
HP
19 tháng 3 2021
ĐK: \(x\ge0\)
Dễ thấy \(1-\sqrt{2\left(x^2-x+1\right)}\le1-\sqrt{2}< 0\)
Khi đó bất phương trình tương đương:
\(x-\sqrt{x}\le1-\sqrt{2\left(x^2-x+1\right)}\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(x+\dfrac{1}{x}-1\right)}\le0\)
\(\Leftrightarrow\sqrt{x}-\dfrac{1}{\sqrt{x}}-1+\sqrt{2\left(\sqrt{x}-\dfrac{1}{\sqrt{x}}\right)^2+2}\le0\)
\(\Leftrightarrow t-1+\sqrt{2t^2+2}\le0\)
T
1
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 1 2024
ĐKXĐ: \(x\ge1\)
Đặt \(\left\{{}\begin{matrix}\sqrt[]{x-1}=a\ge0\\\sqrt[3]{2-x}=b\end{matrix}\right.\) \(\Rightarrow a^2+b^3=1\)
Ta được hệ:
\(\left\{{}\begin{matrix}a+b=1\\a^2+b^3=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}b=1-a\\a^2+b^3=1\end{matrix}\right.\)
\(\Rightarrow a^2+\left(1-a\right)^3=1\)
\(\Leftrightarrow a^3-4a^2+3a=0\)
\(\Leftrightarrow a\left(a-1\right)\left(a-3\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a=0\\a=1\\a=3\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}\sqrt[]{x-1}=0\\\sqrt[]{x-1}=1\\\sqrt[]{x-1}=3\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\\x=10\end{matrix}\right.\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2020
1.
\(2x+1\ge0\Rightarrow x\ge-\dfrac{1}{2}\)
Khi đó pt đã cho tương đương:
\(x^2+2x+2m=\left(2x+1\right)^2\)
\(\Leftrightarrow x^2+2x+2m=4x^2+4x+1\)
\(\Leftrightarrow3x^2+2x+1=2m\)
Xét hàm \(f\left(x\right)=3x^2+2x+1\) trên \([-\dfrac{1}{2};+\infty)\)
\(-\dfrac{b}{2a}=-\dfrac{1}{3}< -\dfrac{1}{2}\)
\(f\left(-\dfrac{1}{2}\right)=\dfrac{3}{4}\) ; \(f\left(\dfrac{1}{3}\right)=\dfrac{2}{3}\)
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi \(\dfrac{2}{3}< 2m\le\dfrac{3}{4}\)
\(\Leftrightarrow\dfrac{1}{3}< m\le\dfrac{3}{8}\)
\(\Rightarrow P=\dfrac{1}{8}\)
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2020
3.
Đặt \(x^2=t\ge0\Rightarrow\left[{}\begin{matrix}x=\sqrt{t}\\x=-\sqrt{t}\end{matrix}\right.\)
Pt trở thành: \(t^2-3mt+m^2+1=0\) (1)
Pt đã cho có 4 nghiệm pb khi và chỉ khi (1) có 2 nghiệm dương pb
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=9m^2-4\left(m^2+1\right)>0\\t_1+t_2=3m>0\\t_1t_2=m^2+1>0\end{matrix}\right.\) \(\Rightarrow m>\dfrac{2}{\sqrt{5}}\)
Ta có:
\(M=x_1+x_2+x_3+x_4+x_1x_2x_3x_4\)
\(=-\sqrt{t_1}-\sqrt{t_2}+\sqrt{t_1}+\sqrt{t_2}+\left(-\sqrt{t_1}\right)\left(-\sqrt{t_2}\right)\sqrt{t_1}.\sqrt{t_2}\)
\(=t_1t_2=m^2+1\) với \(m>\dfrac{2}{\sqrt{5}}\)
