T
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
11 tháng 11 2021
\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)
T
0
TB
1
29 tháng 7 2023
1:
a: Khi m=1 thì (1) sẽ là x^2+2x-5=0
=>\(x=-1\pm\sqrt{6}\)
b: Δ=(2m)^2-4(-2m-3)
=4m^2+8m+12
=4m^2+8m+4+8=(2m+2)^2+8>=8>0
=>Phương trình luôn có hai nghiệm phân biệt
2:
Thay x=-1 và y=2 vào (P), ta được:
a*(-1)^2=2
=>a=2
A
1
AH
Akai Haruma
Giáo viên
28 tháng 5 2022
Lời giải:
Để pt có 2 nghiệm pb thì $\Delta'=1-(m-1)>0\Leftrightarrow m< 2$
Áp dụng hệ thức Viet:
$x_1+x_2=2$
$x_1x_2=m-1$
Khi đó:
$x_1^2+x_2^2-3x_1x_2=2m^2+|m-3|$
$\Leftrightarrow (x_1+x_2)^2-5x_1x_2=2m^2+|m-3|$
$\Leftrightarrow 2^2-5(m-1)=2m^2+|m-3|$
$\Leftrightarrow 2m^2+5m+|m-3|-9=0$
$\Leftrightarrow 2m^2+5m+3-m-9=0$ (do $m< 2 < 3$)
$\Leftrightarrow 2m^2+4m-6=0$
$\Leftrightarrow m^2+2m-3=0$
$\Leftrightarrow (m-1)(m+3)=0$
$\Rightarrow m=1$ hoặc $m=-3$ (đều tm)
NL
1
21 tháng 10 2021
\(d,ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x-1}=2+\sqrt{x+1}\\ \Leftrightarrow x-1=2+x+1+4\sqrt{x+1}\\ \Leftrightarrow4\sqrt{x+1}=-4\Leftrightarrow x\in\varnothing\left(4\sqrt{x+1}\ge0\right)\\ g,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow x+\sqrt{2x-1}+x-\sqrt{2x-1}+2\sqrt{\left(x+\sqrt{2x-1}\right)\left(x-\sqrt{2x-1}\right)}=2\\ \Leftrightarrow2x+2\sqrt{x^2-2x+1}=2\\ \Leftrightarrow\sqrt{\left(x-1\right)^2}=\dfrac{2-2x}{2}=1-x\\ \Leftrightarrow\left|x-1\right|=1-x\\ \Leftrightarrow\left[{}\begin{matrix}x-1=1-x\left(x\ge1\right)\\x-1=x-1\left(x< 1\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x\in R\end{matrix}\right.\)
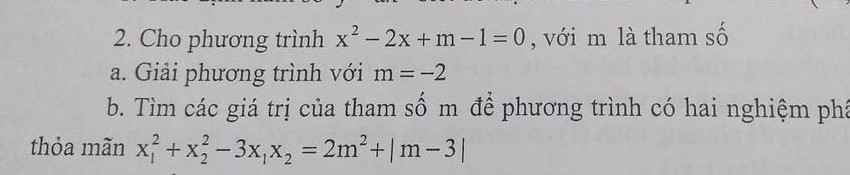
a.
ĐKXĐ: \(x\ge2\)
\(\dfrac{\sqrt{x}-\sqrt{x-1}}{\left(\sqrt{x}+\sqrt{x-1}\right)\left(\sqrt{x}-\sqrt{x-1}\right)}+\dfrac{\sqrt{x-1}-\sqrt{x-2}}{\left(\sqrt{x-1}+\sqrt{x-2}\right)\left(\sqrt{x-1}-\sqrt{x-2}\right)}=1\)
\(\Leftrightarrow\dfrac{\sqrt{x}-\sqrt{x-1}}{1}+\dfrac{\sqrt{x-1}-\sqrt{x-2}}{1}=1\)
\(\Leftrightarrow\sqrt{x}-\sqrt{x-2}=1\)
\(\Leftrightarrow\sqrt{x}=1+\sqrt{x-2}\)
\(\Leftrightarrow x=1+x-2+2\sqrt{x-2}\)
\(\Leftrightarrow2\sqrt{x-2}=1\)
\(\Leftrightarrow x-2=\dfrac{1}{4}\)
\(\Rightarrow x=\dfrac{9}{4}\)
b
ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-2\sqrt{x-1}+1}+\sqrt{x-1+2\sqrt{x-1}+1}=\dfrac{x-1}{2}\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-1\right)^2}+\sqrt{\left(\sqrt{x-1}+1\right)^2}=\dfrac{x-1}{2}\)
\(\Leftrightarrow\left|\sqrt{x-1}-1\right|+\left|\sqrt{x-1}+1\right|=\dfrac{x-1}{2}\)
Đặt \(\sqrt{x-1}=t\ge0\Rightarrow\left|t-1\right|+\left|t+1\right|=\dfrac{t^2}{2}\)
TH1: \(0\le t\le1\) pt trở thành:
\(1-t+t+1=\dfrac{t^2}{2}\Rightarrow t^2=4\)
\(\Rightarrow\left[{}\begin{matrix}t=2>1\left(ktm\right)\\t=-2< 0\left(ktm\right)\end{matrix}\right.\)
TH2: \(t>1\) pt trở thành:
\(t-1+t+1=\dfrac{t^2}{2}\Rightarrow t^2=2t\Rightarrow\left[{}\begin{matrix}t=0< 1\left(ktm\right)\\t=2\end{matrix}\right.\)
\(\Rightarrow\sqrt{x-1}=2\Rightarrow x=5\)