K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
1 tháng 3 2017
\(\sqrt[n]{y}=4x+1\)
\(y^{\dfrac{1}{n}}=4x+1\)
đạo cấp 1
\(\dfrac{1}{n}y^{\left(\dfrac{1}{n}-1\right)}=\dfrac{1}{n}\sqrt[n]{y^{\left(1-n\right)}}=4\)
thay y=(4x+1)^n vào
\(\dfrac{1}{n}\sqrt[n]{\left(4x+1\right)^{n\left(1-n\right)}}=\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}\)
từ đó: \(y'=\dfrac{4}{\dfrac{1}{n}\left(4x+1\right)^{\left(1-n\right)}}=4.n\left(4x+1\right)^{n-1}\)
Có đúng không: cấp n có thể phải làm lấy vài cái--> quy luật nào đó
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2021
Đáy là bát giác đều (8 cạnh) nên chóp có 8 mặt bên
Cộng thêm mặt đáy nữa nên ta sẽ có tổng cộng 9 mặt
KB
3 tháng 5 2022
\(y=tan\left(\sqrt{x^2+4}\right)\Rightarrow y'=\dfrac{1}{cos^2\left(\sqrt{x^2+4}\right)}.\left(\sqrt{x^2+4}\right)'\)
\(\left(\sqrt{x^2+4}\right)'=\dfrac{1}{2\sqrt{x^2+4}}\left(x^2+4\right)'=\dfrac{2x}{2\sqrt{x^2+4}}=\dfrac{x}{\sqrt{x^2+4}}\)
Suy ra : \(y'=\dfrac{x}{cos^2\left(\sqrt{x^2+4}\right).\sqrt{x^2+4}}\)
NT
6
HP
20 tháng 9 2021
3.
\(y=\dfrac{1-sin^24x}{5}=\dfrac{cos^24x}{5}\)
\(cos4x\in\left[-1;1\right]\Rightarrow cos^24x\in\left[0;1\right]\Rightarrow y\in\left[0;\dfrac{1}{5}\right]\Rightarrow\left\{{}\begin{matrix}y_{min}=0\\y_{max}=\dfrac{1}{5}\end{matrix}\right.\)
HP
20 tháng 9 2021
6.
\(y=sinx+cosx+2=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\)
\(sin\left(x+\dfrac{\pi}{4}\right)\in\left[-1;1\right]\Rightarrow y=\sqrt{2}sin\left(x+\dfrac{\pi}{4}\right)+2\in\left[-\sqrt{2}+2;\sqrt{2}+2\right]\)
\(\Rightarrow y_{min}=-\sqrt{2}+2\)
\(y_{max}=\sqrt{2}+2\)
1
E
14 tháng 12 2021
Câu d có thể liệt kê ra, hoặc làm như sau:
Dễ dàng nhận ra với lần đầu tiên tung ra mặt có số chấm là 1,2,5,6 thì chỉ có 1 khả năng để 2 lần cách nhau 2 chấm là 3,4,3,4
Còn với các chấm 3 và 4 xuất hiện ở lần đầu thì có 2 khả năng tung lần 2 để 2 lần gieo cách nhau 2 chấm
Như vậy n(C) = 4.1 + 2.2 = 8
HP
18 tháng 2 2022
\(\lim\limits_{x\rightarrow3}\left(\dfrac{1}{x}-\dfrac{1}{3}\right)\dfrac{1}{\left(x-3\right)^3}=\lim\limits_{x\rightarrow3}\dfrac{1}{3x\left(x-3\right)^2}=+\infty\)
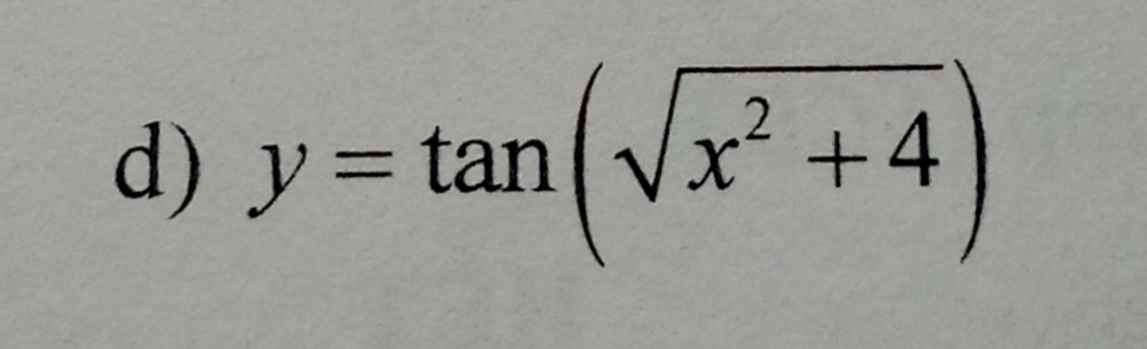
ì làm giùm mình câu này với ạ
\(\left(cotx\right)^{ln\left(1+x^2\right)}=\left(tanx\right)^{-ln\left(1+x^2\right)}=e^{ln\left[\left(tanx\right)^{-ln\left(1+x^2\right)}\right]}\)
\(=e^{-ln\left(tanx\right).ln\left(1+x^2\right)}\sim e^{-ln\left(x\right).x^2}=e^{-\dfrac{lnx}{x^{-2}}}\)
L'Hopital (bạn tự hiểu là giới hạn khi x->0): \(e^{-\dfrac{1}{-2x.x^{-3}}}=e^{\dfrac{x^2}{2}}=e^0=1\)