Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

trong ΔDEFΔDEF vuông tại D có
DK2=EK.KFDK2=EK.KF(đlý)⇒KF=DK2EK=628⇒KF=DK2EK=628=4,5
ta có:EF=EK+KF=8+4,5=12,5
DE2=EF.EK(đlý)DE2=EF.EK(đlý)=12,5.8=100⇒DE=10⇒DE=10
DF2=EF.KFDF2=EF.KF(đlý)=12,5.4,5=56,25⇒⇒DF=7,5

trong \(\Delta DEF\) vuông tại D có
\(DK^2=EK.KF\)(đlý)\(\Rightarrow KF=\dfrac{DK^2}{EK}=\dfrac{6^2}{8}\)=4,5
ta có:EF=EK+KF=8+4,5=12,5
\(DE^2=EF.EK\left(đlý\right)\)=12,5.8=100\(\Rightarrow DE=10\)
\(DF^2=EF.KF\)(đlý)=12,5.4,5=56,25\(\Rightarrow\)DF=7,5

trong \(\Delta DEF\) vuông tại D có
\(DK^2=EK.KF\)(đlý)\(\Rightarrow KF=\dfrac{DK^2}{EK}=\dfrac{6^2}{8}\)=4,5
ta có:EF=EK+KF=8+4,5=12,5
\(DE^2=EF.EK\left(đlý\right)\)=12,5.8=100\(\Rightarrow DE=10\)
\(DF^2=EF.KF\)(đlý)=12,5.4,5=56,25\(\Rightarrow\)DF=7,5



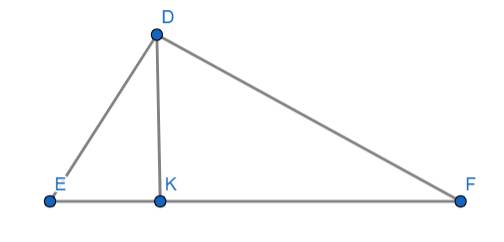
Xét ta có:
\(EF^2=7,5^2=56,25\left(cm\right)\) (1)
Mà: \(DF^2+DE^2=4,5^2+6^2=56,25\left(cm\right)\) (2)
Từ (1) và (2) ta có:
\(EF^2=DE^2+DF^2\)
\(\Rightarrow\Delta DEF\) vuông tại D có đường cao DK
a) Áp dụng hệ thức hai cạnh góc vuông và đường cao ta có:
\(\dfrac{1}{DK^2}=\dfrac{1}{DE^2}+\dfrac{1}{DF^2}\)
\(\Rightarrow DK^2=\dfrac{DE^2DF^2}{DF^2+DF^2}\Rightarrow DK=\sqrt{\dfrac{DE^2DF^2}{DF^2+DE^2}}\)
\(\Rightarrow DK=\sqrt{\dfrac{4,5^2\cdot6^2}{4,5^2+6^2}}=3,6\left(cm\right)\)
b) Áp dụng hệ thức hình chiếu và cạnh góc vuông ta có:
\(\left\{{}\begin{matrix}DE^2=EF\cdot EK\\DF=EF\cdot FK\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{DE^2}{EF}\\FK=\dfrac{DF^2}{EF}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}EK=\dfrac{6^2}{7,5}=4,8\left(cm\right)\\FK=\dfrac{4,5^2}{7,5}=2,7\left(cm\right)\end{matrix}\right.\)
a: Xét ΔDEF có EF^2=DE^2+DF^2
nên ΔDEF vuông tại D
Xét ΔDEF vuông tại D có DK là đường cao
nên DK*FE=DE*DF
=>DE*7,5=27
=>DE=3,6cm
b: ΔDEF vuông tại D có DK là đường cao
nên EK*EF=ED^2
=>EK=6^2/7,5=4,8cm
FK=7,5-4,8=2,7cm

a/ Ta có CF vuông góc AB tại F (gt)
Nên góc CFB = 90 độ
BE vuông góc AC tại E
Nên góc BEC = 90 độ
Tứ giác CEFB có hai đỉnh kề F và E cùng nhìn cạnh BC dưới một góc vuông . Do đó tứ giác CEFB nt
Ta có góc BFC = 90(cmt) độ nên tam giác BFC vuông tại F .
góc BEC = 90 độ (cmt)
Nên tam giác BEC vuông tại E
Tam giác vuông BFC và BEC đều có BC là cạnh huyền nên tâm của đường tròn ngoại tiếp tứ giác là trung điểm của cạnh BC .
Giả sử 2 tam giác đòng dạng là ABC và DEF
Chu vi tam giác ABC : DEF=7:3
=> AB:DE=7:3
AB-DE=10
=> TA có hpt
3AB-7DE=0
AB-DE=10
AB=17.5
DE=7.5
bạn xem lại đề nhé, nếu xét tam giác EKD vuông tại K theo pytago thì cạnh huyền bé hơn cạnh góc vuông nhé