K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
12 tháng 7 2018
Hướng dẫn giải:
Thay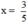 
vào 2 vế của phương trình
Ta được:
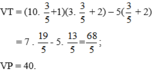
⇒ VT ≠ VP
Vậy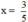 
không là nghiệm của phương trình đã cho.
CM
10 tháng 4 2017
Ta có:
5 x 2 − 2 x + 10 2 = 3 x 2 + 10 x − 8 2 ⇔ 5 x 2 − 2 x + 10 2 − 3 x 2 + 10 x − 8 2 = 0 ⇔ 5 x 2 − 2 x + 10 + 3 x 2 + 10 x − 8 5 x 2 − 2 x + 10 − 3 x 2 − 10 x + 8 = 0 ⇔ 8 x 2 + 8 x + 2 2 x 2 − 12 x + 18 = 0 ⇔ 2 4 x 2 + 4 x + 1 .2 x 2 − 6 x + 9 = 0 ⇔ 2 x + 1 2 x − 3 2 = 0 ⇔ 2 x + 1 2 = 0 x − 3 2 = 0 ⇔ 2 x + 1 = 0 x − 3 = 0 ⇔ x = − 1 2 x = 3
Vậy tập nghiệm của phương trình là S = − 1 2 ; 3
Đáp án cần chọn là: C
PT
1
CM
8 tháng 12 2017
Tại x = 2 ta có:
Vế trái = 2(2 + 2) – 7 = 2.4 – 7 = 8 – 7 = 1
Vế phải = 3 – x = 3 – 2 = 1
⇒ vế trái = vế phải = 1 nên x = 2 có là một nghiệm của phương trình
T
1
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 4 2021
\(\Leftrightarrow5\left(x^4+2x^2+1\right)+2\left(y^6+2y^3+1\right)=13\)
\(\Leftrightarrow5\left(x^2+1\right)^2+2\left(y^3+1\right)^2=13\)
\(\Leftrightarrow\left(x^2+1\right)^2=\dfrac{13-2\left(y^3+1\right)^2}{5}\le\dfrac{13}{5}< 4\)
\(\Rightarrow x^2+1< 2\Rightarrow x^2< 1\)
\(\Leftrightarrow x=0\)
\(\Rightarrow y^6+2y^3-3=0\Rightarrow\left[{}\begin{matrix}y^3=1\Rightarrow y=1\\y^3=-3\left(ktm\right)\end{matrix}\right.\)
Vậy \(\left(x;y\right)=\left(0;1\right)\)
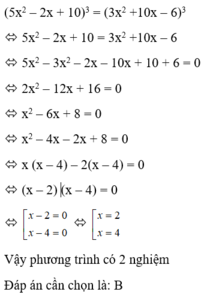
10\(x\) - 3 = 7
10\(x\) = 7 + 3
10\(x\) = 10
\(x\) = 10 : 10
\(x\) = 1
Vậy \(x\) = 1 hay phương trình 10\(x\) - 3 = 7 có nghiệm là 1
10x -3 = 7
10x = 7+3
10x = 10
x = 10:10
Phương trình có nghiệm bằng 1
x = 1