NH
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HA
0
MT
1
4 tháng 6 2015
MIK giải đc nhưng ngại lắm , mỏi tay ,đáp số nè:
\(\left(x^2-x-1\right)\left(2x^2+5x-2\right)\)
21 tháng 7 2018
Phân tích đa thức thành nhân tử bằng phương pháp đặt nhân tử chung
(3x + 2)^2 + (3x - 2)^2 - 2(9x^2 - 4)
\(=\left(3x+2\right)^2-2\left(3x+2\right)\left(3x-2\right)+\left(3x-2\right)^2\)
\(=\left(3x+2-\left(3x-2\right)\right)^2\)
\(=\left(3x+2-3x+2\right)^2\)
\(=4^2\)
\(=16\)
21 tháng 7 2018
\(\left(3x+2\right)^2+\left(3x-2\right)^2-2\left(9x^2-4\right)\)
\(=\left(3x+2\right)^2+\left(3x-2\right)^2-2.\left(3x-2\right)\left(3x+2\right)\)
\(=\left(3x+2-3x+2\right)^2\)
\(=4^2=16\)
FT
1
2 tháng 11 2016
\(\left(x^2-3x+2\right)\left(x^2-9x+20\right)-40=\left(x-1\right)\left(x-2\right)\left(x-4\right)\left(x-5\right)-40\)
\(=\left(x^2-6x+5\right)\left(x^2-6x+8\right)-40\)
Đặt \(t=x^2-6x+5\) thì ta có \(t\left(t+3\right)-40=t^2+3t-40=\left(t+8\right)\left(t-5\right)\)
Suy ra \(\left(x^2-6x+5\right)\left(x^2-6x+8\right)-40=\left(x^2-6x+13\right)\left(x^2-6x\right)=x\left(x-6\right)\left(x^2-6x+13\right)\)
VT
0
3 tháng 9 2016
Đặt \(P\left(x\right)=2x^4+3x^3-9x^2-3x+2\)
Giả sử nhân tử của P(x) có dạng : \(P\left(x\right)=2\left(x^2+ax+b\right)\left(x^2+cx+d\right)=\left(x^2+ax+b\right)\left(2x^2+2cx+2d\right)\)
Khai triển : \(P\left(x\right)=2x^4+2cx^3+2dx^2+2ax^3+2acx^2+2adx+2bx^2+2bcx+2bd\)
\(=2x^4+x^3\left(2c+2a\right)+x^2\left(2d+2ac+2b\right)+x\left(2ad+2cb\right)+2bd\)
Dùng phương pháp hệ số bất định :
\(\Rightarrow\begin{cases}2a+2c=3\\2ac+2b+2d=-9\\2ad+2bc=-3\\bd=1\end{cases}\) . Giải ra được \(\begin{cases}a=-1\\b=-1\\c=\frac{5}{2}\\d=-1\end{cases}\)
Vậy \(P\left(x\right)=2\left(x^2-x-1\right)\left(x^2+\frac{5}{2}x-1\right)=\left(x^2-x-1\right)\left(2x^2+5x-2\right)\)
NL
1
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
15 tháng 12 2023
\(3x^2-6x+9x^2=12x^2-6x=6x\left(2x-1\right)\)
KW
0
19 tháng 7 2021
a) \(x^3+9x^2+27x+27=\left(x+3\right)^3\)
b) \(3\sqrt{3x^3}+18x^2+12\sqrt{3x}+8=\left(\sqrt{3x}+2\right)^3\)
c) \(\dfrac{1}{4}-x^2=\left(\dfrac{1}{2}-x\right)\left(\dfrac{1}{2}+x\right)\)
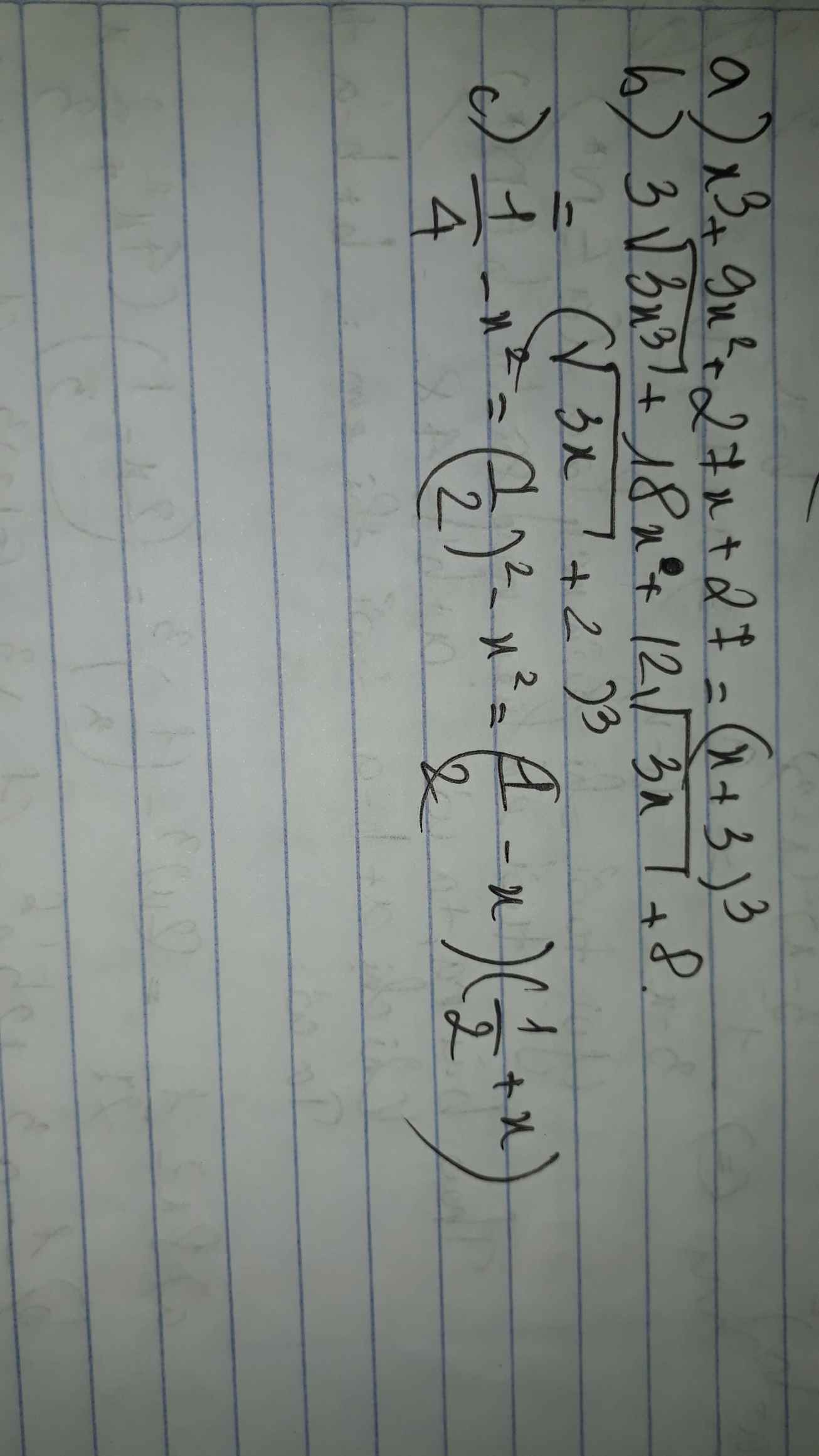
=(3x+2)^2+(3x-2)^2-2(3x-2)(3x+2)
=(3x+2-3x+2)^2
=4^2
=16