Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đường thẳng đi qua hai điểm (1;0) và (0;2) có phương trình là : x 1 + y 2 = 1 ⇔ 2 x + y - 2 = 0
Điểm O(0; 0) thuộc miền bị gạch và 2.0+ 0 – 2 < 0 nên nửa mặt phẳng không bị gạch sọc biểu diễn miền nghiệm của bất phương trình : 2x + y – 2 > 0
Đáp án là D.

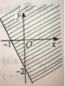
Đường thẳng đi qua hai điểm (-1 ; 0 ) và (0 ; -2) có phương trình chính tắc là »
x - 1 + y - 2 = 1 ⇔ 2 x + y + 2 = 0
Điểm O(0; 0) thuộc miền bị gạch và 2.0 + 0 + 2 >0 .
Do đó, nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2 x + y + 2 ≤ 0
(kể cả bờ là đường thẳng).

Đường thẳng đi qua hai điểm (-1 ; 0 ) và (0 ; -2) có phương trình chính tắc là »
x - 1 + y - 2 = 1 ⇔ 2 x + y + 2 = 0
Điểm O(0; 0) thuộc miền bị gạch và 2.0 + 0 + 2 >0 .
Do đó, nửa mặt phẳng không bị gạch biểu diễn miền nghiệm của bất phương trình 2 x + y + 2 ≤ 0
(kể cả bờ là đường thẳng 2x+y+2=0).
Chọn C

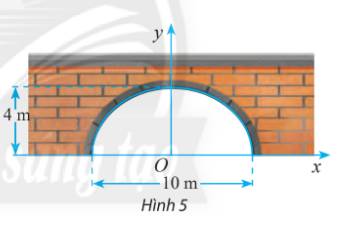
Chiều cao là 4 m tương ứng với \(b = 4\)
Chiều rộng bằng 10 m nên \(2a = 10 \Rightarrow a = 5\)
Vậy phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{16} = 1\)

Tham khảo:
a)
Miền nghiệm của bất phương trình \(x \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(x = 0\). Đây là trục Oy.
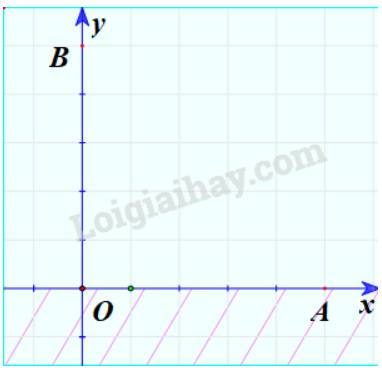
Bước 2: Lấy điểm A(150;0) không thuộc trục Oy và thay vào biểu thức \(x\), ta được: \(x = 150 \ge 0\).
Bước 3: Do điểm A thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm A.
Minh họa (phần không bị gạch chéo):

Miền nghiệm của bất phương trình \(y \ge 0\)
Bước 1: Vẽ đường thẳng (nét liền) \(y = 0\). Đây là trục Ox.
Bước 2: Lấy điểm B(0;150) không thuộc trục Ox và thay vào biểu thức \(y\), ta được: \(y = 150 \ge 0\).
Bước 3: Do điểm B thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm B.
Minh họa (phần không bị gạch chéo):
Miền nghiệm của bất phương trình \(x + y \le 150\):
Bước 1: Vẽ đường thẳng (nét liền) \(x + y = 150\).
Bước 2: Lấy điểm O(0;0) không thuộc đường thẳng \(x + y = 150\) và thay vào \(x + y\), ta được: \(0 + 0 = 0 \le 150\)
Bước 3: Do điểm O thỏa mãn bất phương trình nên miền nghiệm của bất phương trình là nửa mặt phẳng có chứa điểm O.
Minh họa (phần không bị gạch chéo):
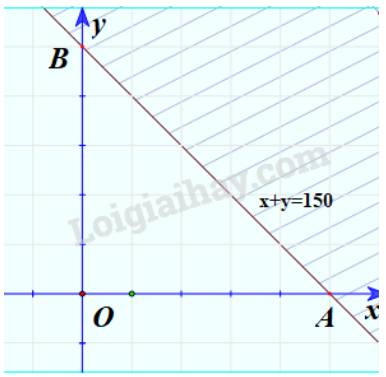
Vậy \({D_1}\) là nửa trên mặt phẳng có bờ là trục Oy, \({D_2}\) là nửa bên phải mặt phẳng có bờ là trục Ox và \({D_3}\) là nửa mặt phẳng có bờ là đường thẳng x+y=150 chứa điểm O.
b) Vẽ tất cả các miền miền \({D_1},{D_2}\) và \({D_3}\) lên cùng một mặt phẳng.

=>Miền tam giác OAB (H.2.5) có phải là giao điểm của các miền \({D_1},{D_2}\) và \({D_3}\)
c) Lấy một điểm trong tam giác OAB (chẳng hạn điểm (1;2)) hoặc một điểm trên cạnh nào đó của tam giác OAB (chẳng hạn điểm (1;149)) và kiểm tra xem tọa độ của các điểm đó có phải là nghiệm của hệ bất phương trình sau hay không:
\(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;2) trong tam giác OAB, thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{1 \ge 0}\\
{2 \ge 0}\\
{1 + 2 \le 150}
\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;2) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Lấy điểm (1;149), thay vào hệ \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)
Ta được:
\(\left\{ {\begin{array}{*{20}{l}}
{1 \ge 0}\\
{149 \ge 0}\\
{1 + 149 \le 150}
\end{array}} \right.\) (luôn đúng)
Vậy điểm (1;149) là nghiệm của hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + y \le 150\end{array} \right.\)

Vì ABCD là hình bình hành nên ta có: \(\overrightarrow {AD} = \overrightarrow {BC} \)\(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \) (đpcm)

Có 7 trận: Tứ kết 1, Tứ kết 2, Tứ kết 3, Tứ kết 4, Bán kết 1, Bán kết 2, Chung kết.

Miền góc không bị gạch được giới hạn bởi hai đường thẳng:
Đường thẳng thứ nhất đi qua hai điểm (6;0) và (0;2) nên có phương trình:
x 6 + y 2 = 1 ⇔ x + 3 y - 6 = 0
Với bờ là đường thẳng x+3y-6=0 theo hình thì gạch bỏ đi phần không chứa O
Do đó nửa mặt phẳng không gạch (chứa O) với bờ là x+3y-6=0 biểu diễn nghiệm của bất phương trình x+3y-6=<0.
Đường thẳng thứ hai đi qua hai điểm (-2;0) và (0;-4) nên có phương trình:
x - 2 + y - 4 = 1 ⇔ 2 x + y + 4 = 0
Với bờ là đường thẳng 2x+y+4=0 theo hình thì gạch bỏ đi phần chứa O
Do đó nửa mặt phẳng không gạch (không chứa O) với bờ là 2x+y+4=0 biểu diễn nghệm của bất phương trình 2x+y+4<0.
Kết hợp 2 miền ta được miền góc không bị gạch là nghiệm của hệ
x + 3 y - 6 < 0 2 x + y + 4 < 0
Chọn đáp án D.

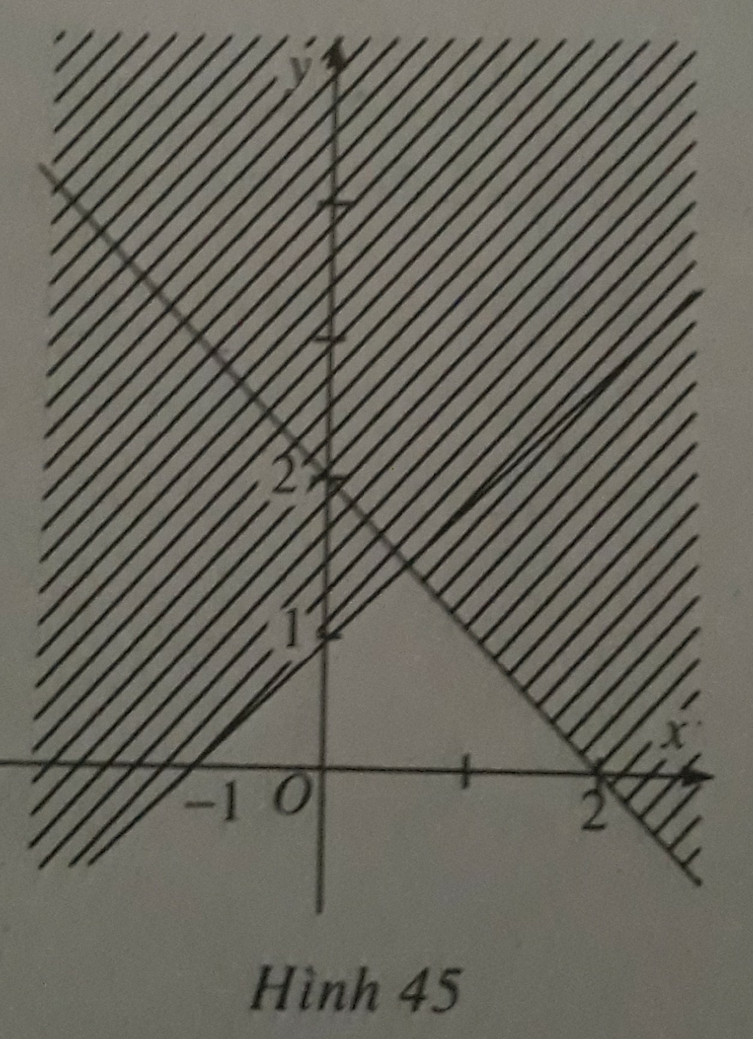
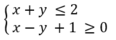 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.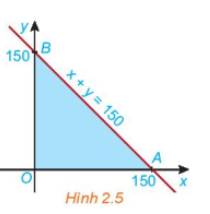



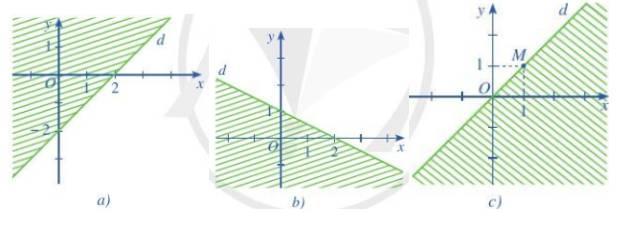
a) Đường thẳng qua điểm (2;0) và (0;-2) nên phương trình đường thẳng là \(x-y-2=0\)
Lấy điểm (3;0) thuộc miền nghiệm ta có 3-0-2=1>0
=> Bất phương trình cần tìm là \(x - y - 2 > 0\)
b) Đường thẳng qua điểm (2;0) và (0;1)
Thay x=2, y=0 vào phương trình \(y = ax + b\) ta được \(0 = 2a + b\)
Thay x=0, y=1 vào phương trình \(y = ax + b\) ta được \(1 = 0.a + b\)
=> \(a = - \frac{1}{2},b = 1\)
=> phương trình đường thẳng là \(y = - \frac{1}{2}x + 1\)
Lấy điểm (3;0) thuộc miền nghiệm ta có \( - \frac{1}{2}x + 1 - y = \frac{{ - 1}}{2} < 0\)
=> Bất phương trình cần tìm là \( - \frac{1}{2}x - y + 1 < 0\)
c) Đường thẳng qua điểm (0;0) và (1;1) nên phương trình đường thẳng là
x-y=0
Lấy điểm (0;1) thuộc miền nghiệm ta có x-y=-1<0
=> Bất phương trình cần tìm là \(x - y < 0\)