Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

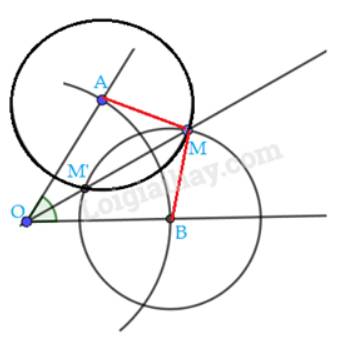
Ta có: AM = bán kính đường tròn tâm A
BM = bán kính đường tròn tâm B
Mà 2 đường tròn này có bán kính bằng nhau
Do đó, AM = BM
Xét \(\Delta \)OAM và \(\Delta \)OBM có:
OA = OB( = bán kính đường tròn tâm O)
MA = MB (cmt)
OM chung
\( \Rightarrow \) \(\Delta \)OAM = \(\Delta \)OBM ( c.c.c)
\( \Rightarrow \) \(\widehat {AOM} = \widehat {BOM}\) ( 2 góc tương ứng)
Mà OM nằm giữa 2 tia OA và OB
\( \Rightarrow \) OM là tia phân giác của góc AOB.

Xin lỗi bạn nhé mình không vẽ hai hình tròn đè lên nhau được nha
Điểm I nằm trên đường tròn (B, BO) nên BI = BO.
Theo giả thiết AO = BO nên:
AI =BI = AO =BO.
Hai tamm giác OAI và OBI có ba cạnh bằng nhau từng đôi một: OA = OB, AI = BI và OI chung,nên chúng bằng nhau. Ta suy ra \(\widehat{AOI}=\widehat{BOI}\)nghĩa là tia OI là tia phân giác của góc xOy.

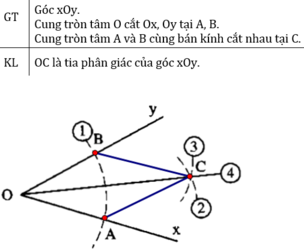
Nối BC, AC
ΔOBC và ΔOAC có:
OB = OA (bán kính)
AC = BC (gt)
OC cạnh chung
Nên ΔOBC = ΔOAC (c.c.c)
nên OC là tia phân giác của góc xOy.

a) Ta có đường tròn tâm A có bán kính bằng đưởng tròn tâm B. Vậy bán kính đường tròn tâm A = bán kính đường tròn tâm B => AI=BI
Xét tam giác AOI và tam giác BOI, ta có:
OA=OB(gt)
AI=BI
OI: cạnh ching
Do đó tam giác AOI = tam giác BOI
=> Góc AOI = góc BOI
Vậy OI là tia phân giác cảu góc xOy (đpcm)
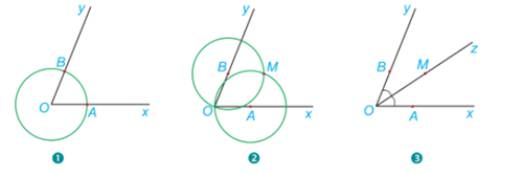
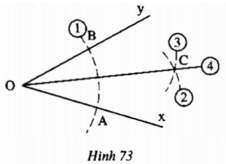
Xét \(\Delta OBM\) và \(\Delta OAM\) có:
\(OA = OB( = R)\)
OM chung
AM=BM (do hai đường tròn tâm A và B có bán kính bằng nhau)
\( \Rightarrow \)\(\Delta OBM\) = \(\Delta OAM\)(c.c.c)
\( \Rightarrow \) \(\widehat {MOB} = \widehat {MOA}\) (hai góc tương ứng)
Mà tia OM nằm trong góc xOy
Vậy OM là tia phân giác của góc xOy.