
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tham khảo
Trong toán học, định lý khai triển nhị thức (ngắn gọn là định lý nhị thức) là một định lý toán học về việc khai triển hàm mũ của tổng. Cụ thể, kết quả của định lý này là việc khai triển một nhị thức bậc {\displaystyle n}

{\displaystyle (x+a)^{n}=\sum _{k=0}^{n}{n \choose k}x^{n-k}a^{k}}
với:
{\displaystyle {n \choose k}={\frac {n!}{(n-k)!k!}}}
Gọi là số tổ hợp chập k của n phần tử.
Định lý này đã được độc lập chứng minh bởi hai người đó là:
Nhà toán học và cơ học Isaac Newton tìm ra trong năm 1665.Nhà toán học James Gregory tìm ra trong năm 1670.Công thức đã giới thiệu còn mang tên là Nhị thức Newton.

Các bất đẳng thức nổi tiếng
- Bất đẳng thức Bunyakovsky.
- Bất đẳng thức Azuma.
- Bất đẳng thức Bernoulli.
- Bất đẳng thức Boole.
- Bất đẳng thức Cauchy-Schwarz.
- Bất đẳng thức cộng Chebyshev.
- Bất đẳng thức Chernoff.
- Bất đẳng thức Cramer-Rao
- :333
Tôi đã học :
-bất đảng thức cô-si
-bất đảng thức bunyakovsky
về phần ví dụ thì tui chịu nha
Quên hết rùi


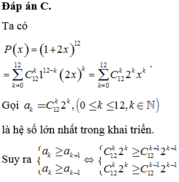



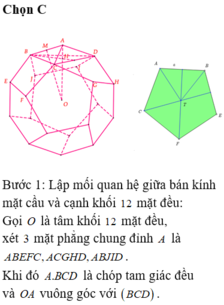
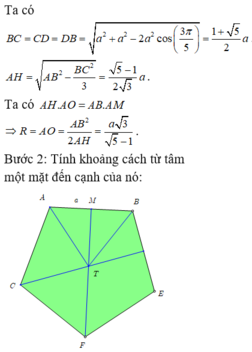
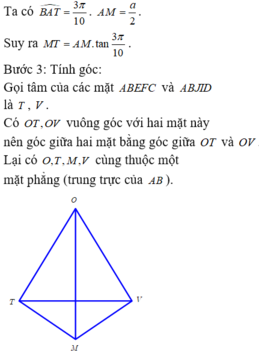
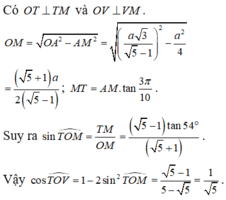
Tham khảo :
Nhị thức Newton là 1 công thức khai triển hàm mũ của tổng. Cụ thể là khai triển một nhị thức bậc n ((a+b)n) thành một đa thức có n+1 số hạng.
HT
Công thức