Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(l=\frac{K\lambda}{2}=\frac{Kv}{2f}\)
\(\Rightarrow f=\frac{Kv}{21}\)
\(\Rightarrow f_{min}=\frac{v}{21}=\frac{\left(K+1\right)v}{21}-\frac{Kv}{21}=f_2-f_1=50Hz\)
\(\rightarrow D\)

Đáp án C
Sóng dừng trên dây có hai đầu cố định có tần số f = n v 21
Theo bài ra ta có ( n + 1 ) v 21 - n v 21 = 200 - 150 → v 21 = 50
→ tốc độ truyền sóng trên dây là v = 50.2l = 50.2.0,75 = 75 m/s.
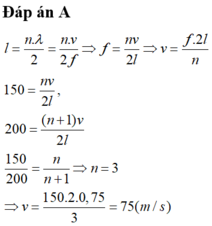
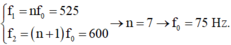
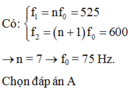
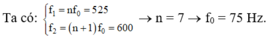

2 đầu dây cố định, có sóng dừng, suy ra: \(l=k\frac{\curlywedge}{2}\)
suy ra: \(f=\frac{kv}{2l}\)
theo đề có \(\frac{\left(k+1\right)v}{2l}\)=200Hz và \(\frac{kv}{2l}\)=150Hz
\(\frac{\left(k+1\right)v}{2l}\)-\(\frac{kv}{2l}\)=\(\frac{v}{2l}\)=fmin. Suy ra tần số nhỏ nhất tạo sóng dừng là 50Hz