Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)
\(175\cdot19+38\cdot175+43\cdot175\\ =175\cdot19+175\cdot38+175\cdot43\\ =175\cdot\left(19+38+43\right)\\ =175\cdot100\\ =17500\)
b)
\(125\cdot75+125\cdot13-80\cdot125\\ =125\cdot75+125\cdot13-125\cdot80\\ =125\cdot\left(75+13-80\right)\\ =125\cdot10\\ =125\cdot8\\ =1000\)
a, 175. 19 + 38. 175 + 43. 175
= 175. 19 + 175. 38 + 175. 43
= 175.(19 + 38 + 43)
= 175. 100
= 17500

2/
Xét phân số \(\dfrac{2n-3}{n+1}=\dfrac{2n+2-5}{n+1}=\dfrac{2n+2}{n+1}-\dfrac{5}{n+1}=\dfrac{2\left(n+1\right)}{n+1}-\dfrac{5}{n+1}=2-\dfrac{5}{n+1}\)
\(n\in Z\Rightarrow2n-3\inƯ\left(5\right)=\left\{-1;-5;1;5\right\}\)
Ta có bảng:
| 2n - 3 | -1 | -5 | 1 | 5 |
| n | 1 | -1 | 2 | 4 |
Vậy \(n\in\left\{-1;1;2;4\right\}\)
1/
(x + 1) + (x + 3) + (x + 5) + ... + (x + 999) = 500
<=> (x + x + x + ... + x) + (1 + 3 + 5 + ... + 999) = 500
Xét tổng A = 1 + 3 + 5 + ... + 999
Số số hạng của A là: (999 - 1) : 2 + 1 = 500
Tổng A là: (999 + 1) x 500 : 2 = 250 000
Do A có 500 số hạng nên có 500 ẩn x.
Vậy ta có: 500x + 250 000 = 500
=> 500x = -249 500
=> x = 499
Vậy x = 499


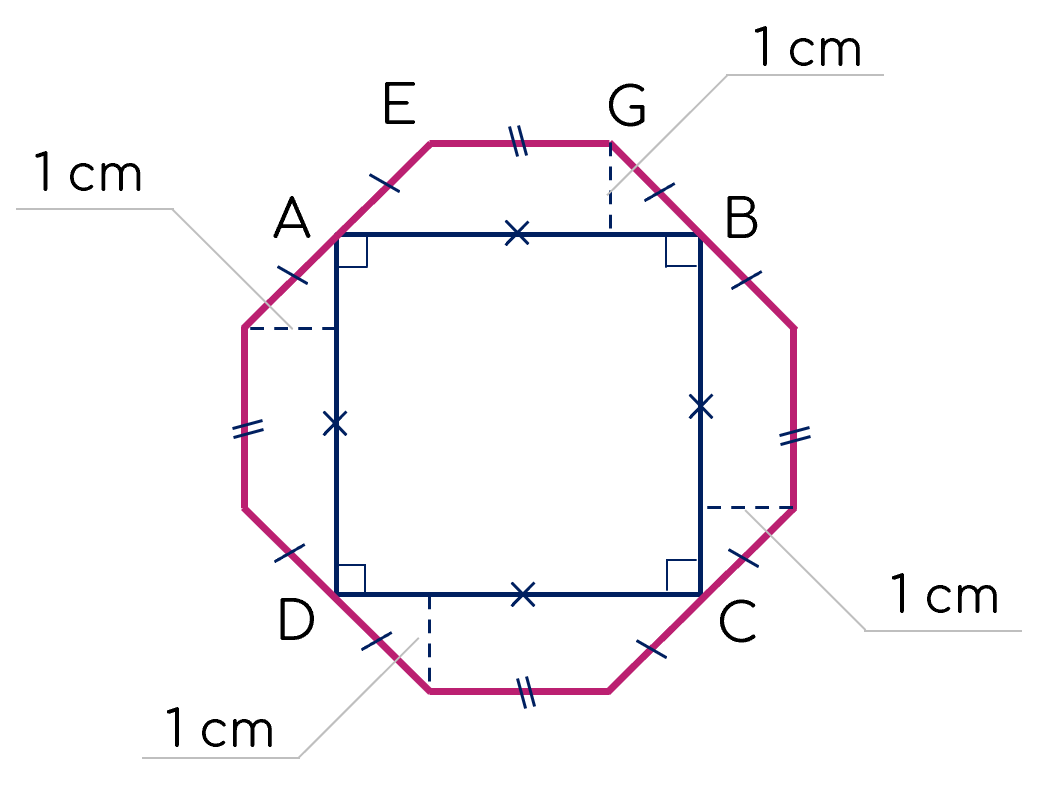
Chu vi hình vuông là 16 cm nên cạnh hình vuông bằng 4 cm
Diện tích hình vuông bằng: 4.4 = 16 cm22.
Diện tích bốn hình thang cân (bằng nhau) phía ngoài hình vuông bằng: 28 - 16 = 12 cm22.
Hình thang cân AEGB có diện tích bằng: 12 : 4 = 3 cm22.

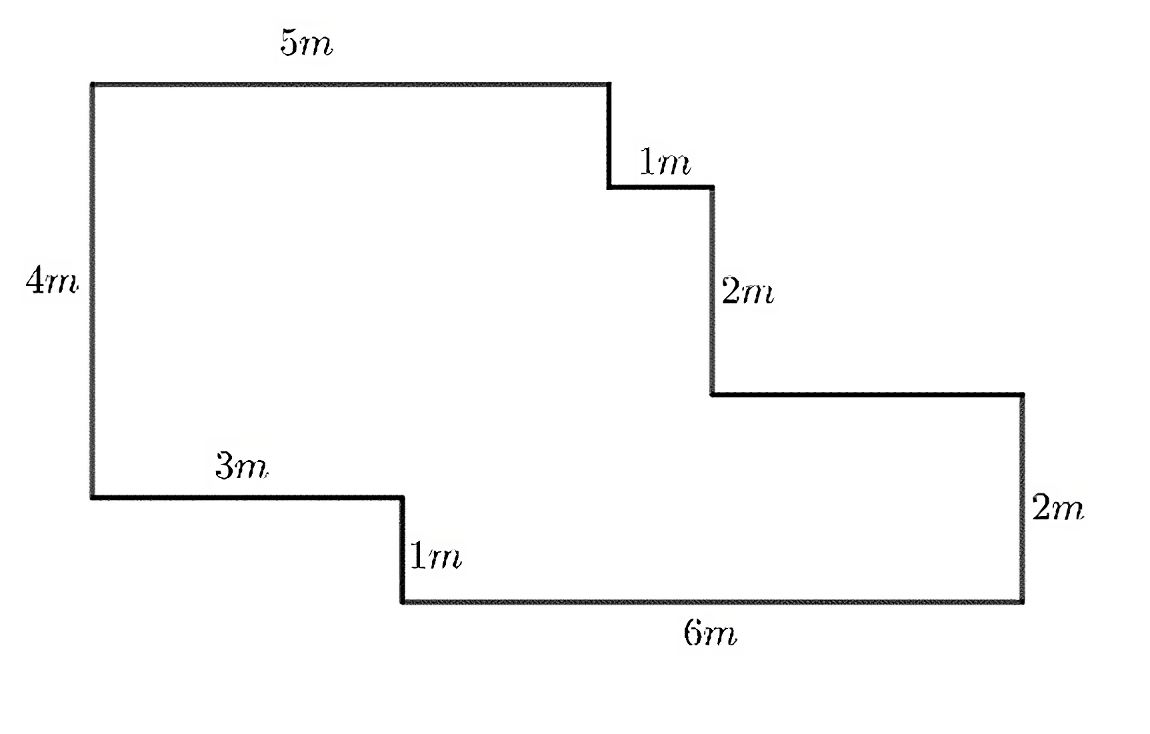
Chia mảnh vườn thành các hình chữ nhật nhỏ. Tính chiều dài, rộng của các hình chữ nhật bé rồi tính diện tích từng hình 1. Cuối cùng cộng diện tích của tất cả các hình chữ nhật vs nhau là xong:))

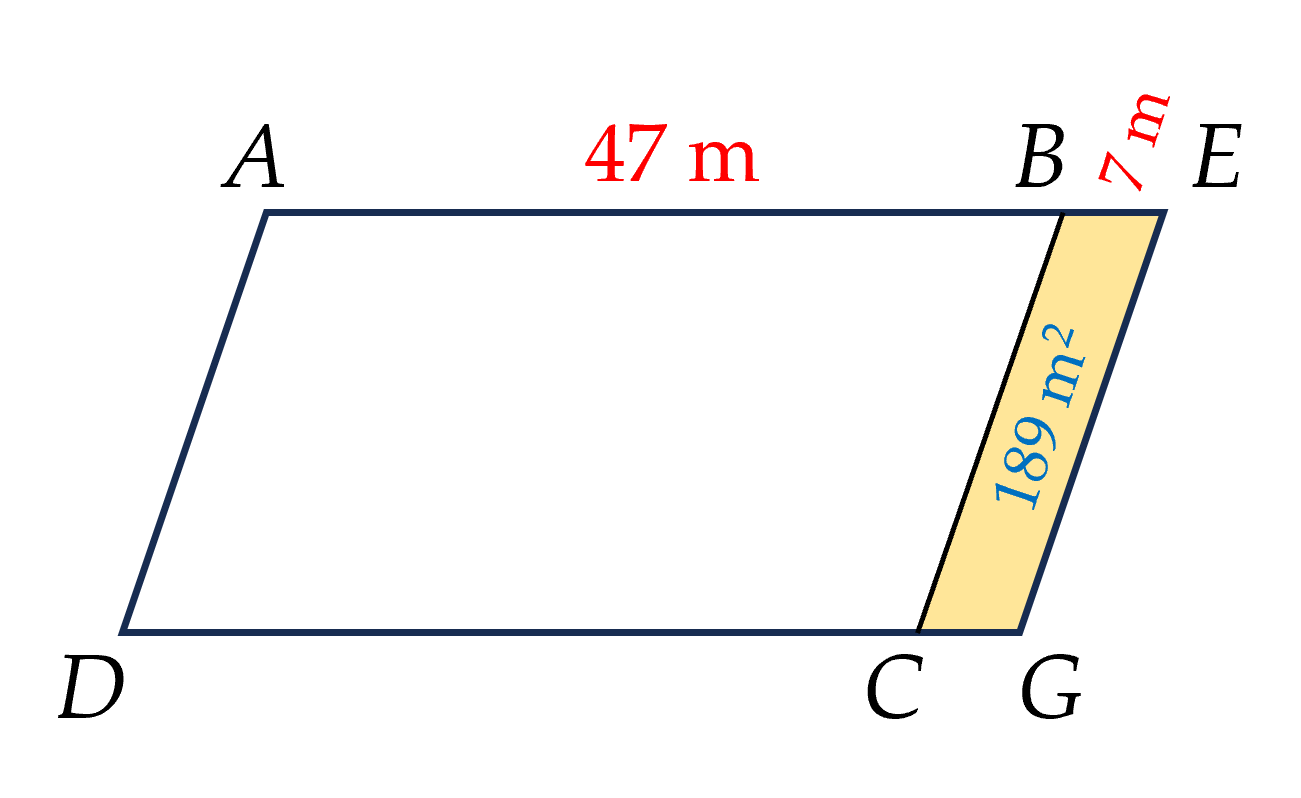
Đường cao hình bình hành là :
189 : 7 = 27 (m)
Diện tích hbh ban đầu là :
27 x 47 = 1269(m^2)

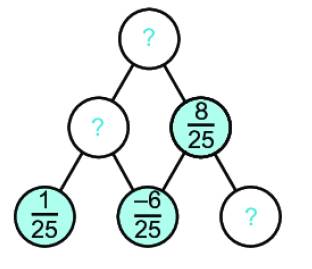
Quy luật: số trong ô ở hàng trên = tổng 2 số trong 2 ô dưới nó
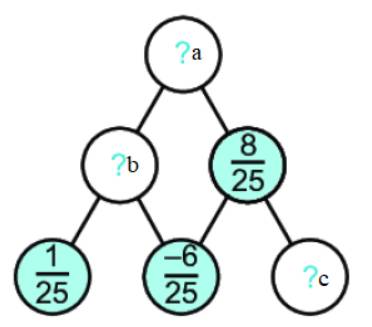
Dấu “?b” ở đây bằng \(\dfrac{1}{{25}} + \dfrac{{ - 6}}{{25}} = \dfrac{{1 + \left( { - 6} \right)}}{{25}} = \dfrac{{ - 5}}{{25}} = \dfrac{{ - 1}}{5}\)
Dấu “?c” ở đây bằng \(\dfrac{8}{{25}} - \dfrac{{ - 6}}{{25}} = \dfrac{{8 - \left( { - 6} \right)}}{{25}} = \dfrac{{14}}{{25}}\)
Dấu “?a” ở đây bằng \(\dfrac{8}{{25}} + \dfrac{{ - 5}}{{25}} = \dfrac{3}{{25}}\)

\(D=\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)...\left(1-\dfrac{1}{99^2}\right)\)
\(D=\dfrac{2^2-1}{2^2}\cdot\dfrac{3^2-1}{3^2}...\cdot\dfrac{99^2-1}{99^2}\)
\(D=\dfrac{\left(2+1\right)\left(2-1\right)}{2^2}\cdot\dfrac{\left(3+1\right)\left(3-1\right)}{3^2}\cdot...\cdot\dfrac{\left(99+1\right)\left(99-1\right)}{99^2}\)
\(D=\dfrac{3\cdot1}{2^2}\cdot\dfrac{4\cdot2}{3^2}\cdot\dfrac{5\cdot3}{4^2}\cdot\dfrac{6\cdot4}{5^2}\cdot...\cdot\dfrac{100\cdot98}{99^2}\)
\(D=\dfrac{1\cdot2\cdot3^2\cdot4^2\cdot5^2\cdot6^2\cdot...\cdot98^2\cdot99\cdot100}{2^2\cdot3^2\cdot...\cdot99^2}\)
\(D=\dfrac{2\cdot99\cdot100}{2^2\cdot99^2}\)
\(D=\dfrac{100}{2\cdot99}\)
\(D=\dfrac{50}{99}\)
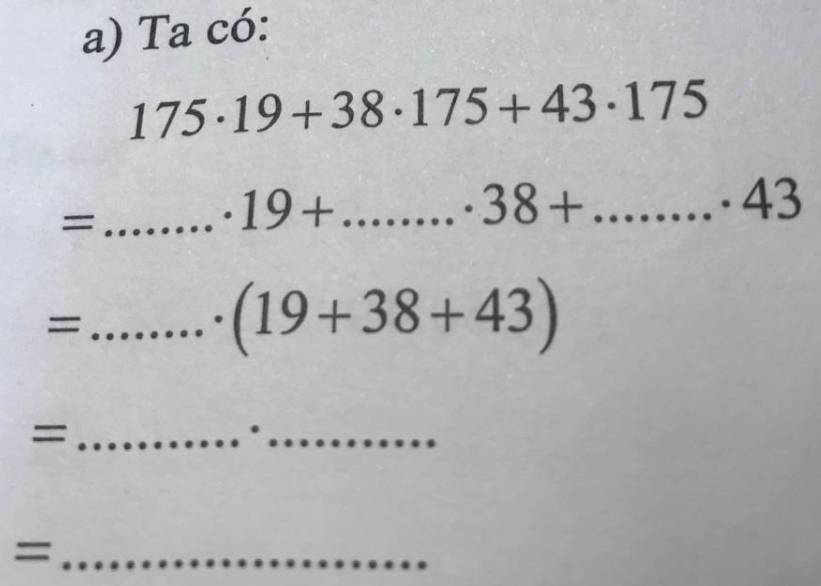
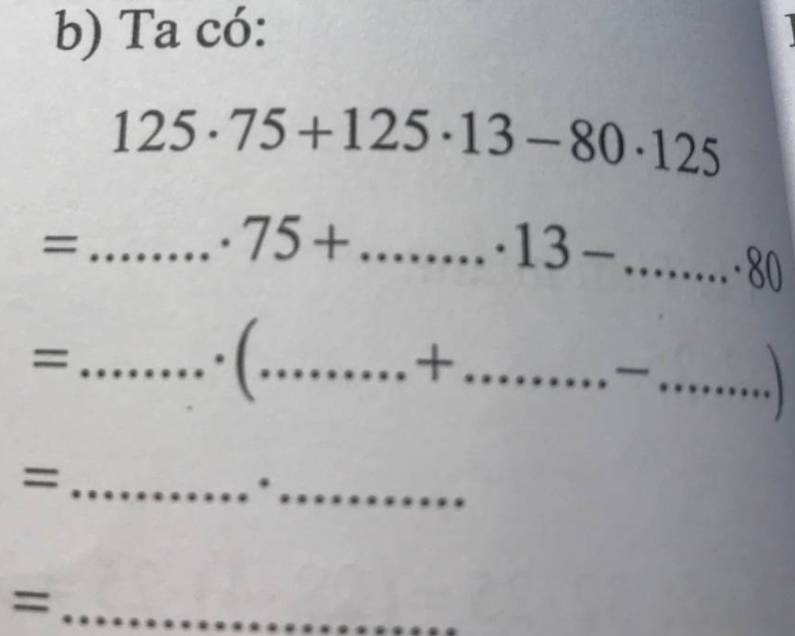
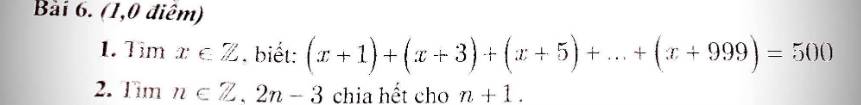

 Nam dự định làm một mô hình cột cờ với các kích thước như hình trên bằng bìa cứng. Tính diện tích giấy bìa tối thiểu cần dùng, biết lá cờ là hình chữ nhật có kích thước 3cm x 2cm
Nam dự định làm một mô hình cột cờ với các kích thước như hình trên bằng bìa cứng. Tính diện tích giấy bìa tối thiểu cần dùng, biết lá cờ là hình chữ nhật có kích thước 3cm x 2cm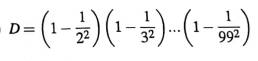
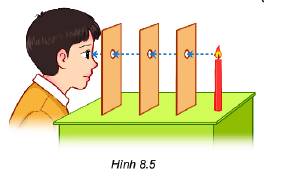
Vì người đó nhìn được ngọn nến nên giữa mắt người đó đến ngọn nến không có vật cản. Do đó, các lỗ hổng cùng nằm trên một đường thẳng.
Có