Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì khối lượng ô tô không đổi, lực trong hai trường hợp là như nhau nên gia tốc như nhau. Ta có:
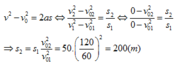
=> Chọn D

Chọn A
Xét vật dao động chịu tác dụng của lực quán tính. Khi đó vật có VTCB bị lệch ra khỏi phương thẳng đứng.
Độ dài của dây treo là:
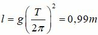
Tại vị trí cân bằng mới, VTCB mới lệch đi góc a tính bởi tana»a/g» 5 0 Đến đây, dao động của vật được mô tả lại như sau: Vật dao động với VTCB lệch so với phương thẳng đứng góc 5 0 , ban đầu vật ở biên, có chu kì mới xác định bởi
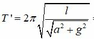
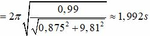
Thời gian lần thứ 9 vật qua vị trí phương dây treo thẳng đứng là 8,5T’»16,93s
Trong các đáp án, chỉ có đáp án A có giá trị thời gian gần đúng nhất. Nên có thể loại trừ các đáp khác mà không cần tính vận tốc

Đáp án A
Áp dụng công thức cộng vận tốc ta có
![]()
Ta có hai xe đi theo hai hướng vuông góc nhau
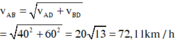
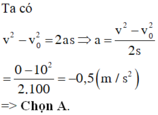
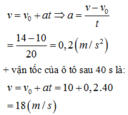
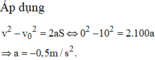


A B C
Cho AB là khoảng cách từ ô tô đến điểm gặp
AC là khoảng cách người đó tới điểm gặp ( mặt đường)
BC là khoảng cách của ô tô và người đó
Xét tam giác vuông ABC vuông tại A
Theo định lí py ta go ta có
AB2+AC2=BC2
=> AB=\(\sqrt{BC^2-AC^2}\)
=> AB =\(\sqrt{130^2-50^2}=120\left(m\right)\)
hay quãng đường ô tô phải đi để đến điểm gặp là 120(m)
Thời gian để cả 2 gặp nhau là:
t=\(\frac{s_{AB}}{v_{ôtô}}=\frac{120}{10}=12\left(s\right)\)
Vận tốc người đó phải đi là
v=\(\frac{s_{AC}}{t}=\frac{50}{12}=4.17\)(m/s)
Gọi \(S\) là quãng đường ô tô đi đến chỗ người đó đón
\(S_1\) là khoảng cách chỗ người đó đang đứng đến nới ô tô đang đứng
\(S_2\) là khoảng cách từ chỗ người đó đến quãng đường
\(S=\sqrt{S_1^2-S_2^2}=\sqrt{130^2-50^2}=120\left(m\right)\)
Thời gian ô tô đi đến chỗ đón là :
\(t=\dfrac{S}{V_1}=\dfrac{120}{10}=12\left(s\right)\)
Vận tốc ô tô chạy để có thể gặp ô tô là:
\(V_2=\dfrac{S_2}{t}=\dfrac{50}{12}=4,16\)(m/s)