Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.
a) Đổi 5 km/h = \(\frac{{25}}{{18}}\)m/s; 29 km/h = \(\frac{{145}}{{18}}\)m/s; 49 km/h = \(\frac{{245}}{{18}}\); 30 km/h = \(\frac{{25}}{3}\)m/s
+ Gia tốc trong đoạn đường 1: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{25}}{{18.1}} = \frac{{25}}{{18}} \approx 1,39(m/{s^2})\)
+ Gia tốc trong đoạn đường 2: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{145}}{{18}} - \frac{{25}}{{18}}}}{{4 - 1}} \approx 2,22(m/{s^2})\)
+ Gia tốc trong đoạn đường 3: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{245}}{{18}} - \frac{{145}}{{18}}}}{{6 - 4}} \approx 2,78(m/{s^2})\)
+ Gia tốc trong đoạn đường 4: \(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{\frac{{25}}{3} - \frac{{245}}{{18}}}}{{7 - 6}} \approx - 5,28(m/{s^2})\)
b) Trong 4 đoạn đường trên, vận tốc tăng dần, còn gia tốc từ đoạn đường 1 đến đoạn đường 3 tăng dần, nhưng từ đoạn đường 3 đến đoạn đường 4 thì gia tốc giảm dần.
2.
Gia tốc của con báo là:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{9 - 30}}{3} = - 7(m/{s^2})\)

a) Hình lấy từ nguồn khác.
b)
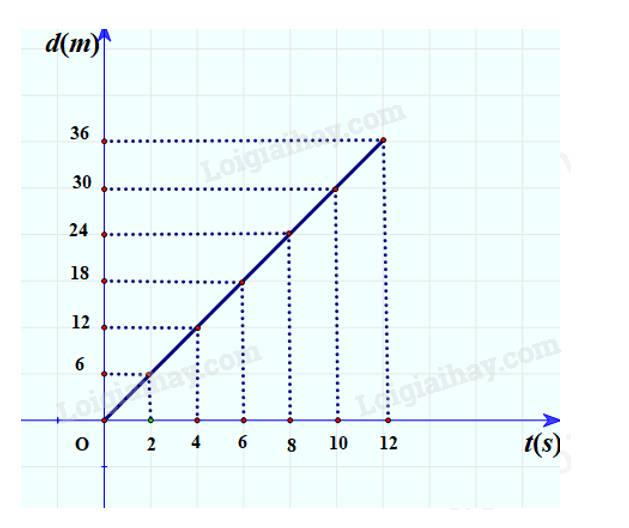
- Từ t = 0,0 s đến t = 5,0 s người B đi được 10 m.
- Sau thời điểm t = 5,0 s người B đi với tốc độ không đổi là 4 m/s
+ Quãng đường người B đi được sau 1 s đi với tốc độ 4 m/s là: 10 + 4.1 = 14 m
+ Quãng đường người B đi được sau 2 s đi với tốc độ 4 m/s là: 10 + 4.2 = 18 m (đuổi kịp người A)
=> Người B đuổi kịp người A sau 2 s đi với tốc độ không đổi là 4m/s.
c)
Người B đi được 8 m trong khoảng thời gian đi với tốc độ không đổi (đến khi gặp nhau).

- Vẽ đồ thị độ dịch chuyển – thời gian: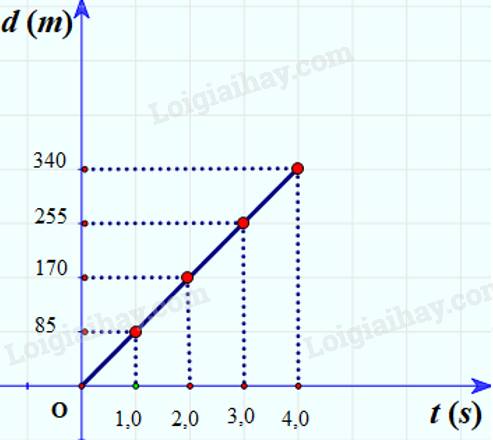
- Vận tốc của xe là:
\(v=\dfrac{d}{t}=85\left(m/s\right)\)

1.
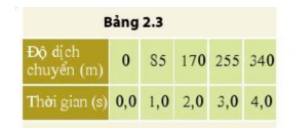
Từ đồ thị ta thấy, trong 25s đầu người đó chuyển động thẳng từ O – A và không đổi chiều, độ dịch chuyển trong 25 s đầu là 50 m.
Suy ra: Mỗi giây người đó bơi được: \(\frac{{50}}{{25}} = 2\left( m \right)\)
Vận tốc của người đó là: \(v = \frac{d}{t} = \frac{{50}}{{25}} = 2\left( {m/s} \right)\)
2.
Từ A – B: người đó không bơi => Người đó không bơi từ giây 25 đến giây 35.

1.
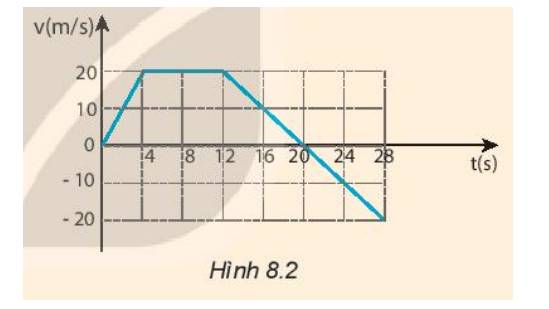
a) Mô tả chuyển động:
- Trong 2 giây đầu tiên: chuyển động thẳng đều với vận tốc 1 m/s.
- Từ giây thứ 2 đến giây thứ 4: chuyển động nhanh dần đều
- Từ giây 4 đến giây 7: chuyển động chậm dần
- Từ giây 4 đến giây 8: dừng lại
- Từ giây 8 đến giây 9: chuyển động nhanh dần theo chiều âm
- Từ giây 9 đến giây 10 chuyển động thẳng đều với vận tốc -1 m/s.
b) Quãng đường đi được và độ dịch chuyển:
- Sau 2 giây:
\({s_1} = {d_1} = {v_1}{t_1} = 1.2 = 2\left( {m/s} \right)\)
- Sau 4 giây:
\({s_2} = {d_2} = {s_1} + \frac{1}{2}(1 + 3).2 = 2 + 4 = 6\left( m \right)\)
- Sau 7 giây:
+ Quãng đường:
\({s_3} = {s_2} + \frac{1}{2}.3.\left( {7 - 4} \right) = 6 + 4,5 = 10,5\left( m \right)\)
+ Độ dịch chuyển:
\({d_3} = {d_2} + \frac{1}{2}.(3).\left( {7 - 4} \right) = 6 + 4,5 = 10,5\left( m \right)\)
- Sau 10 giây:
+ Quãng đường:
\({s_4} = {s_3} + s' = 10,5 + 0,5 + 1 = 12\left( m \right)\)
+ Độ dịch chuyển:
\({d_4} = {d_3} + d' = 10,5 - 0,5 - 1 = 9\left( m \right)\)
* Kiểm tra bằng công thức:
- Sau 2 giây:
\({s_1} = {d_1} = {v_1}{t_1} = 1.2 = 2\left( {m/s} \right)\)
- Sau 4 giây:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{3 - 1}}{{4 - 2}} = \frac{2}{2} = 1\left( {m/{s^2}} \right)\)
\({s_2} = {d_2} = {d_1} + {v_1}{t_1} + \frac{1}{2}at_1^2 = 2 + 1.2 + \frac{1}{2}{.1.2^2} = 6\left( m \right)\)
- Sau 7 giây:
\(a = \frac{{\Delta v}}{{\Delta t}} = \frac{{0 - 3}}{{7 - 4}} = \frac{2}{2} = - 1\left( {m/{s^2}} \right)\)
+ Quãng đường và độ dịch chuyển từ giây 4 đến giây 7 là:
\(d' = s' = {v_0}t + \frac{1}{2}a{t^2} = 3.3 + \frac{1}{2}( - 1).{(7 - 4)^2} = 4,5\left( m \right)\)
=> Quãng đường và độ dịch chuyển đi được sau 7 giây là:
\({d_3} = {s_3} = {d_2} + d' = 6 + 4,5 = 10,5\left( m \right)\)
- Sau 10 giây:
+ Từ giây 7 – 8: đứng yên
+ Từ giây 8 – 9:
\(a = \frac{{ - 1 - 0}}{{9 - 8}} = - 1\left( {m/{s^2}} \right)\)
\(d = {v_0}t + \frac{1}{2}a{t^2} = 0.1 + \frac{1}{2}\left( { - 1} \right){.1^2} = - 0,5\left( m \right)\)
s = 0,5 m
+ Từ giây 9 – 10:
\(d = vt = - 1.1 = - 1\left( m \right)\)
s = 1 m
Suy ra: độ dịch chuyển và quãng đường đi được sau 10 giây lần lượt là:
\({d_4} = {d_3} - 0,5 - 1 = 10,5 - 0,5 - 1 = 9\left( m \right)\)
\({s_4} = {s_3} - 0,5 - 1 = 10,5 + 0,5 + 1 = 12\left( m \right)\)
=> Kiểm tra thấy các kết quả trùng nhau.
2.
a)
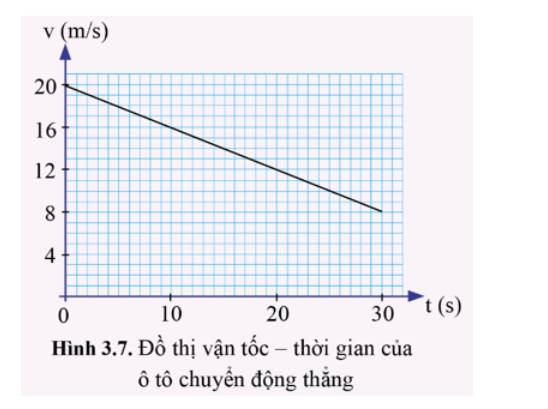
Gia tốc của vận động viên trong đoạn đường sau khi qua vạch đích là:
\({v^2} - v_0^2 = 2{\rm{ad}} \Leftrightarrow a = \frac{{{v^2} - v_0^2}}{{2{\rm{d}}}} = \frac{{{0^2} - {{10}^2}}}{{2.20}} = - 2,5\left( {m/{s^2}} \right)\)
b)
Thời gian vận động viên đó cần để dừng lại kể từ khi cán đích là:
\(a = \frac{{\Delta v}}{{\Delta t}} \Leftrightarrow \Delta t = \frac{{\Delta v}}{a} = \frac{{0 - 10}}{{ - 2,5}} = 4\left( s \right)\)
c)
Vận tốc trung bình của người đó trên quãng đường dừng xe là:
\(v = \frac{d}{t} = \frac{{20}}{4} = 5\left( {m/s} \right)\)
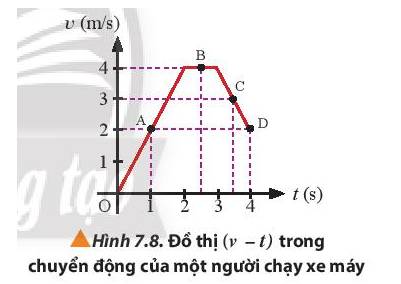
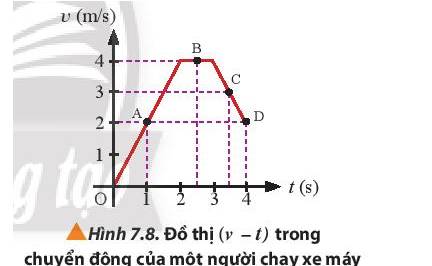

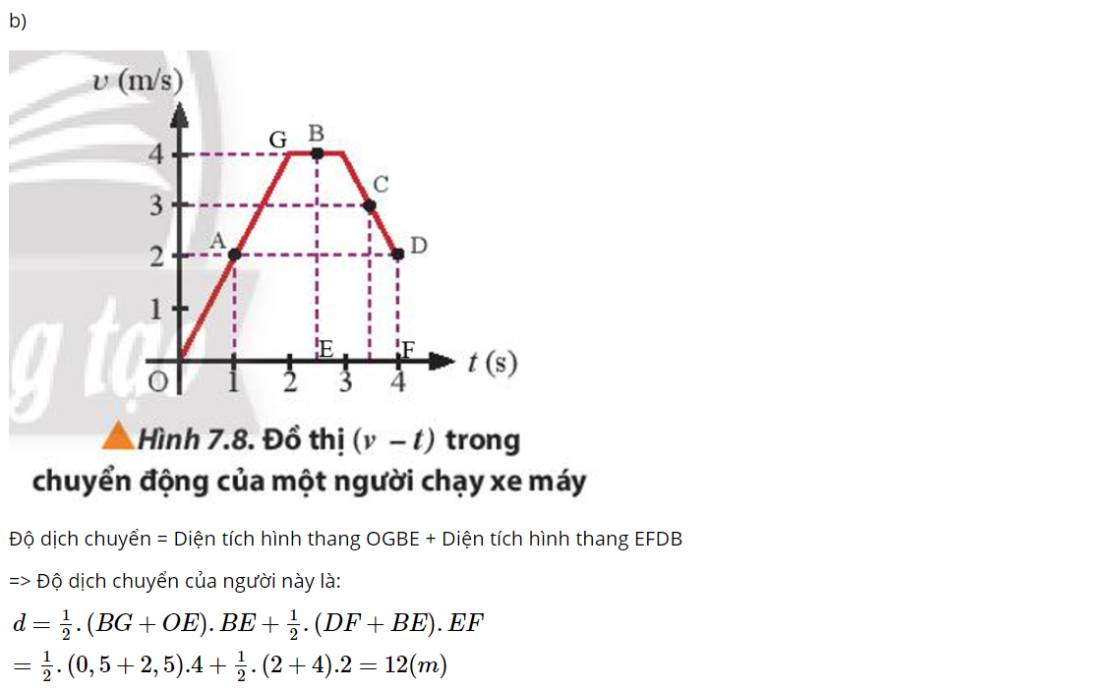





a) Gia tốc của người này tại các thời điểm là:
+ t = 1 s: \(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{2}{1} = 2(m/{s^2})\)
+ t = 2,5 s: \(a = 0 (m/{s^2})\)
+ t = 3,5 s: \(a = \frac{{{v_2} - {v_1}}}{{{t_2} - {t_1}}} = \frac{3-4}{{3,5-3}}=-2(m/{s^2})\)
b)
Độ dịch chuyển = Diện tích hình thang OGBE + Diện tích hình thang BKDH + Diện tích hình chữ nhật HDFE
=> Độ dịch chuyển của người này là:
\(\begin{array}{l}d = \frac{1}{2}.(BG + OE).BE + \frac{1}{2}.(BK + HD).BH\ + (EF.DF)\ = \frac{1}{2}.(0,5 + 2,5).4 + \frac{1}{2}.(0,5 + 1,5).2 + 2.1,5 = 11(m)\end{array}\)