Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: số phần tử của không gian mẫu là Ω = C 40 2
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có: n D = C 20 2 = 190 ;
X: “lấy được 2 bi viên xanh” ta có: n X = C 10 2 = 45 ;
V: “lấy được 2 bi viên vàng” ta có: n V = C 6 2 = 15 ;
T: “ lấy được 2 bi màu trắng” ta có: n T = C 4 2 = 6 .
Ta có D,X,V,T là các biến cố đôi một xung khắc và A = D ∪ X ∪ V ∪ T
Suy ra xác xuất để lấy được 2 viên bi cùng màu là:
P A = P D + P X + P V + P T = 256 C 40 2 = 64 195 .
Chọn đáp án D.

Đáp án B
Hướng dẫn giải:
+ Số cách chọn 1 viên bi xanh: ![]()
+ Số cách chọn 2 viên bi đỏ: ![]()
+ Số cách chọn 5 viên bi trắng: ![]()
+ Số cách chọn 8 viên bi thỏa mãn yêu cầu bài toán: ![]()

Ta có: ![]()
Gọi các biến cố: D: “lấy được 2 bi viên đỏ” ta có ![]()
X: “lấy được 2 bi viên xanh” ta có: ![]()
V: “lấy được 2 bi viên vàng” ta có: ![]()
T: “ lấy được 2 bi màu trắng” ta có : ![]()
Ta có D; X; V; T là các biến cố đôi một xung khắc và A= D ∪ X ∪ V ∪ T
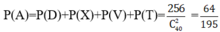
Chọn B.

Có \(C_{24}^3\) cách chọn 3 viên bất kì.
Có \(C_8^3+C_6^3+C_{10}^3\) cách họn 3 viên bi cùng màu.
Có 6 cách chọn 3 viên bi cùng số.
\(\Rightarrow\) Có \(C_{24}^3-\left(C_8^3+C_6^3+C_{10}^3\right)-6=1822\) cách chọn 3 viên bi khác màu, khác số.
Chọn 1 viên xanh: có 6 cách
Chọn 1 viên đỏ khác số viên xanh: 7 cách
Chọn 1 viên vàng khác số viên xanh và đỏ: 8 cách
Tổng cộng: \(6.7.8=336\) cách

Không gian mẫu là chọn ngẫu nhiên mỗi hộp 2 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 4 viên bi được chọn luôn có bi đỏ nhưng không có bi xanh . Ta liệt kê các trường hợp thuận lợi của không gian biến cố A như sau:
● Trường hợp 1. Chọn hộp thứ nhất 2 viên bi đỏ, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 2. Chọn hộp thứ nhất 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi từ 8 viên bi (2 đỏ và 6 vàng), có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
● Trường hợp 3. Chọn hộp thứ nhất 2 viên bi vàng, có ![]() cách.
cách.
Chọn hộp thứ hai 2 viên bi đỏ hoặc 1 viên bi đỏ và 1 viên bi vàng, có ![]() cách.
cách.
Do đó trường hợp này có ![]() cách.
cách.
Suy ra số phần tử của biến cố A là ![]()
Vậy xác suất cần tính 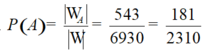
Chọn B.

Ta có, số phần tử của không gian mẫu n ( Ω ) = C 10 2
Gọi các biến cố: D: “lấy được 2 viên đỏ” ; X: “lấy được 2 viên xanh” ;
V: “lấy được 2 viên vàng”
Ta có D, X, V là các biến cố đôi một xung khắc và C = D ∪ X ∪ V
P ( C ) = P ( D ) + P ( X ) + P ( V ) = C 4 2 C 10 2 + C 3 2 C 10 2 + C 2 2 C 10 2 = 2 9
Chọn đáp án B

Không gian mẫu là số sách lấy tùy ý 2 viên từ hộp chứa 12 viên bi.
Suy ra số phần tử của không gian mẫu là ![]() .
.
Gọi A là biến cố 2 viên bi được lấy vừa khác màu vừa khác số .
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi đỏ là 4.4=16 cách (do số bi đỏ ít hơn nên ta lấy trước, có 4 cách lấy bi đỏ. Tiếp tục lấy bi xanh nhưng không lấy viên trùng với số của bi đỏ nên có 4 cách lấy bi xanh).
● Số cách lấy 2 viên bi gồm: 1 bi xanh và 1 bi vàng là 3.4=12cách.
● Số cách lấy 2 viên bi gồm: 1 bi đỏ và 1 bi vàng là 3.3=9 cách.
Suy ra số phần tử của biến cố A là 16+12+9=37.
Vậy xác suất cần tính 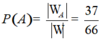 .
.
Chọn B.
Theo mình nghĩ là chọn 4 viên bi cùng màu mà nhỉ
Tổng các cách chọn 4 bi đỏ, 4 bi xanh, 4 bi trắng, 4 bi vàng:
\(C_{10}^4+C_{25}^4+C_6^4+C_9^4=10977\) (cách)