
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


số 0 là đơn thức không có bậc
2.\(\sqrt{2}\)
1/Số không là đơn thức không có bậc
2/ A B C D 1
Đường chéo đó chia hình vuông là 2 nửa,mỗi nữa chính là một tam giác vuông.
Do mỗi cạnh của hình vuông bằng 1.Áp dụng định lí Pytagore cho tam giác vuông ABC (hay DBC cũng được),ta có:
\(BC^2=AC^2+AB^2=1+1=2\Rightarrow BC=\sqrt{2}\)
Vậy độ dài đường chéo là \(\sqrt{2}\)

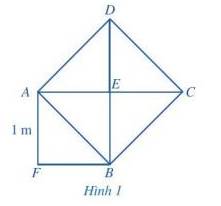
a) Ta có: \({S_{ABCD}} = 4.{S_{AEB}}\) = 4. \(\frac{1}{2}.1.1\) = 2 (m2)
b) AB = \(\sqrt {S{}_{ABCD}} = \sqrt 2 \) (m)
a: AC=DB=2m
S ABCD=1/2*2*2=2m2
b: AB=căn 1^2+1^2=căn 2(m)

Ta có: Bình phương độ dài đường chéo của một hình chữ nhật là: \({5^2} + {8^2} = 25 + 64 = 89\)
Độ dài đường chéo của một hình chữ nhật là: \(\sqrt {89} = 9,43398...\)(dm)
Làm tròn kết quả này đến hàng phần mười, ta được: 9,4 dm
Chú ý: Độ dài đường chéo của một hình chữ nhật bằng căn bậc hai số học của tổng các bình phương độ dài hai cạnh của nó

Độ dài đường chéo của hình chữ nhật là:
\(\sqrt{7^2+6^2}=\sqrt{49+36}=\sqrt{85}\simeq9,2\left(dm\right)\)

a: ABCD là hình vuông
=>AB=BC=CD=DA và \(\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{ADC}=90^0\) và AC là phân giác của \(\widehat{DAB}\) và DB là phân giác của góc ADC; BD là phân giác của góc ABC
AC là phân giác của góc DAB
=>\(\widehat{CAB}=\dfrac{1}{2}\widehat{DAB}=\dfrac{1}{2}\cdot90^0=45^0\)
AEBF là hình vuông
=>AB là phân giác của \(\widehat{FAE}\) và \(\widehat{FAE}=90^0\)
=>\(\widehat{BAE}=\dfrac{1}{2}\cdot\widehat{EAF}=45^0\)
\(\widehat{BAE}=45^0\)
\(\widehat{BAC}=45^0\)
Do đó: \(\widehat{BAE}=\widehat{BAC}=45^0\)
=>AE và AC là hai tia trùng nhau
=>A,E,C thẳng hàng
BD là phân giác của góc ABC
=>\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
AEBF là hình vuông
=>BA là phân giác của góc EBF
=>\(\widehat{ABE}=\dfrac{1}{2}\cdot\widehat{FBE}=45^0\)
=>\(\widehat{ABE}=\widehat{ABD}\)
=>BE,BD là hai tia trùng nhau
=>B,E,D thẳng hàng
B,E,D thẳng hàng
A,E,C thẳng hàng
Do đó: BD cắt AC tại E
ADCB là hình vuông
=>AC=BD và AC vuông góc với BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại E và E là trung điểm chung của AC và DB
E là trung điểm của AC nên AC=2AE=2(cm)
E là trung điểm của BD nên BD=2EB=2(cm)
Xét tứ giác ADCB có DB\(\perp\)AC
nên \(S_{ADCB}=\dfrac{1}{2}\cdot DB\cdot AC=\dfrac{1}{2}\cdot2\cdot2=2\left(cm^2\right)\)
b: ADCB là hình vuông
=>\(S_{ADCB}=AB^2\)
=>\(AB^2=2\)
=>\(AB=\sqrt{2}\left(cm\right)\)

Độ dài đường chéo hình chữ nhật là:
\(\sqrt{7^2+6^2}\) = \(\sqrt{83}\) = 9,1(dm)
Kết luận :.....
\(\sqrt{2}\)
Độ dài đường chéo :\(\sqrt{1.1.2}\)