Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Cơ năng của con lắc E = E d 2 + E t 2 = 0 , 128 J
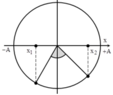
→ Biểu diễ dao động của vật tương ứng trên đường tròn.
+ Từ hình vẽ ta có Δ t = T 360 a r sin − 0 , 5 A A + a r sin 2 A 2 A = π 48
→ T = 0,1π → ω = 20 rad/s
Vậy biên độ dao động của con lắc là A = 2 E m ω 2 = 2.0 , 128 0 , 1.20 2 = 8 c m

Chọn đáp án C
Tại t = t 2 thì:
W đ 2 = W t 2 = 0,064 J => W = 0,128 J.
Tại t 1 = 0 thì:
W đ 1 = 0,096 J => W t 1 = 0,032 J.
W t W = x a 2 ⇒ x = ± A W t W .
Áp dụng vào hai thời điểm
=> x 1 = ± A 2 . và x 2 = ± A 2 .
Theo bài ra, từ t 1 đến t 2 thì động năng tăng đến giá trị cực đại rồi giảm, tức thế năng của con lắc giảm đến 0 rồi tăng, tương ứng với vật đi từ vị trí x 1 = A 2 . qua vị trí cân bằng, đến x 2 = - A 2 . hoặc ngược lại.
Ta xét 1 trường hợp như trên hình vẽ.
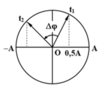
Từ hình vẽ suy ra góc quét:
Δ φ = 5 π 12 ⇒ t = 5 T 24 = π 48
⇒ T = π 10 ⇒ ω = 20 r a d / s
⇒ W = 1 2 m ω 2 A 2 ⇒ A = 8 c m .

W = w d 2 + w t 2 = 0 , 064 + 0 , 064 = 0 , 128 J
![]()
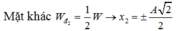
![]()
![]()
Biên độ dao động:


Đáp án B
Phương pháp: Áp dụng công thức tính cơ năng của con lắc lò xo dao động điều hoà
Cách giải:
Cơ năng của con lắc: W = 1 2 mω 2 A 2 = 1 2 . 0 , 1 . 10 2 . π 2 . 0 , 1 2 = 0 , 5 ( J )

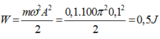
Cơ năng: \(W=0,064+0,096=0,16J\) \(\Rightarrow v_{max}=\sqrt{3,2}\)(m/s)
+ Thời điểm t1: \(v_1=\sqrt{1,92}\)(m/s)
+ Thời điểm t2: \(v_2=\sqrt{1,28}\)(m/s)
Biểu diễn sự biến thiên vận tốc bằng véc tơ quay ta có:
√3,2 √1,28 √1,92 v O M N
Do \(v_1^2+v_2^2=v_{max}^2\) nên OM vuông góc ON.
Như vậy góc quay là \(90^0\)
Thời gian: \(t=\frac{1}{4}T=\frac{\pi}{48}\Rightarrow T=\frac{\pi}{12}\)
\(\Rightarrow\omega=24\)(rad/s)
Biên độ: \(A=\frac{v_{max}}{\omega}=\frac{\sqrt{3,2}}{24}=0,07m=7cm\)
tại t_2 ta có
W_đ/W_t = 1 --> x=A/\eqrt{2}
W_đ = W_t -->W= 2 W_đ =0.128
tại t=0 W_t = W-W_đ =0.032 -->W_đ /W_t =3 hay x =+-A/2
w= 20 rad/s W=1/2w^2*m*A^2 --->A=8
t/12+T/8 =5T/24=\pi/48 -->T=0.1\pi