Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Khoảng thời gian giữa 2 lần liên tiếp động ăng bằng thế năng là T/4
\(\Rightarrow \dfrac{T}{4}=\dfrac{\pi}{40}\)
\(\Rightarrow T = \dfrac{\pi}{10}\)
\(\Rightarrow \omega=\dfrac{2\pi}{T}=20(rad/s)\)
Biên độ dao động: \(A=\dfrac{v_{max}}{\omega}=\dfrac{100}{20}=5(cm)\)
Ban đầu, vật qua VTCB theo chiều dương trục toạ độ \(\Rightarrow \varphi=-\dfrac{\pi}{2}\)
Vậy PT dao động là: \(x=5\cos(20.t-\dfrac{\pi}{2})(cm)\)

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Áp dụng công thức tính năng lượng dao động của con lắc đơn ta có:
\(W_1 = \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}\) và \(W_2 = \dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Theo giả thiết hai con lắc đơn có cùng năng lượng
\(\Rightarrow \dfrac{1}{2}.m_1.g.\ell_1. \alpha_1 ^{2}=\dfrac{1}{2}.m_2.g.\ell_2. \alpha_2 ^{2}\)
Do khối lượng hai con lắc bằng nhau nên:
\(\ell_1.\alpha_1 ^{2} = \ell_2. \alpha_2 ^{2}\)
\(\Rightarrow \alpha_2 = \alpha_1 .\sqrt{l1/l2}\).
Thay số ta tìm được: \(\alpha_2 = 5,625^0\)

Ta có: \(\begin{cases}\Delta l_1=l_1-l_0=\frac{g}{\omega^2_1}\\\Delta l_2=l_2-l_0=\frac{g}{\omega^2_2}\end{cases}\)\(\Rightarrow\frac{\omega^2_2}{\omega^2_1}=\frac{21-l_0}{21,5-l_0}=\frac{1}{1,5}\)\(\Rightarrow l_0=20\left(cm\right)\)
\(\Rightarrow\Delta l_1=0,01\left(m\right)=\frac{g}{\omega^2_1}\Rightarrow\omega_1=10\pi\left(rad/s\right)\)
KQ = 3,2 cm

+ CLLX treo thẳng đứng, khi ở VTCB thì: \(\Delta\ell_0=\dfrac{mg}{k}\) (1)
+ CLLX trên mặt phẳng nghiêng:
P N F α
Vật nằm cân bằng thì: \(\vec{P}+\vec{F}+\vec{N}=\vec{0}\)
Chiếu lên trục tọa độ ta có: \(P.\sin\alpha-F=0\)
\(\Rightarrow mg\sin\alpha=k.\Delta\ell_2\)
\(\Rightarrow \Delta\ell_2=\dfrac{mg\sin\alpha}{k}\) (2)
Từ (1) và (2) ta có: \(\sin\alpha=\dfrac{\Delta \ell_2}{\Delta\ell_1}=\dfrac{3}{5}\)
\(\Rightarrow \alpha =36,9^0\)
 chọn A
chọn A
Bài này có vẻ lẻ quá bạn.
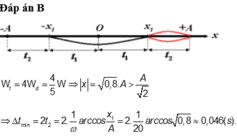
\(W_t=4W_đ\Rightarrow W_đ=\dfrac{W_t}{4}\)
Cơ năng: \(W=W_đ+W_t=W_t+\dfrac{W_t}{4}=\dfrac{5}{4}W_t\)
\(\Rightarrow \dfrac{1}{2}kA^2=\dfrac{5}{4}.\dfrac{1}{2}kx^2\)
\(\Rightarrow x = \pm\dfrac{2}{\sqrt 5}A\)
M N O α α
Thời gian nhỏ nhất ứng với véc tơ quay từ M đến N.
\(\cos\alpha=\dfrac{2}{\sqrt 5}\)\(\Rightarrow \alpha =26,6^0\)
Thời gian nhỏ nhất là: \(\Delta t=\dfrac{26,6\times 2}{360}.T=\dfrac{26,6\times 2}{360}.\dfrac{2\pi}{20}=0.046s\)
bạn ơi cho mình hỏi thời gian nhỏ nhất hay lớn nhất thì cách tính vẫn vậy hả?