Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

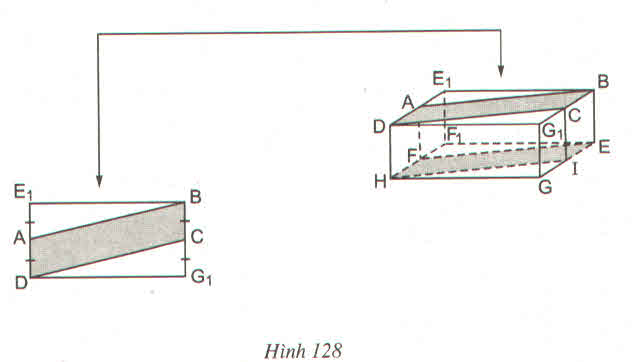
Trải 6 mặt của hình lập phương ABCD.A'B'C'D' như hình bs.18a. Để đi đường ngắn nhất từ M đến M' (M' chính là trung điểm của A'D' trên mặt khai triển) thì con kiến cần bò theo đoạn thẳng MM'. Trên chiếc hộp, đường đi ngắn nhất của con kiến là đường MNPQKZM' như ở hình bs.18b (dễ thấy N, P, Q, K, Z lần lượt là trung điểm của DD', CD, BC, BB', A'B').
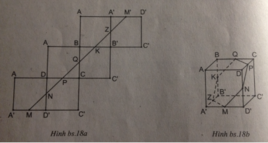

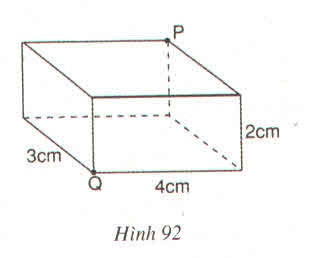
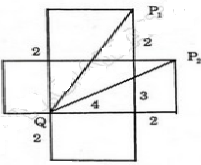
Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.

Bài giải:
a) Ta có AD = CD
nên AD + DB = CD + DB = CB (1) 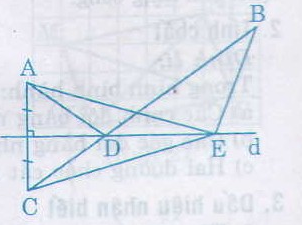
và AE = CE
nên AE + EB = CE + EB (2)
mà CB < CE + EB (3)
Nên từ (1) (2) và (3), suy ra
AD + DB < AE + EB
b) Theo câu a con đường ngắn nhất mà bạn Tú phải đi là con đường ADB

Vì con kiến phải bò theo mặt của hình hộp từ Q đến P tức phải bò trên "một mặt phẳng". Ta vẽ hình khai triển của hình hộp chữ nhật và trải phẳng như sau:
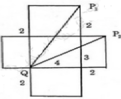
Khi đó, P sẽ có hai vị trí là P1 và P2. Và quãng đường ngắn nhất sẽ là một trong hai đoạn thẳng QP1 hoặc QP2.


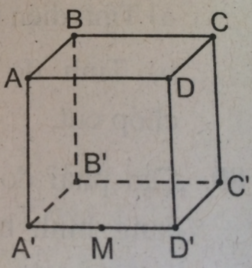
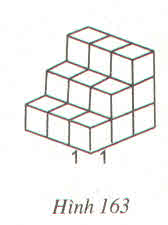
Lớp dưới cùng gồm: 3.3 (hình lập phương đơn vị)
Lớp ở giữa gồm: 3.2 (hình lập phương đơn vị)
Lớp trên cùng: 3 (hình lập phương đơn vị)
Tổng cộng có 9+6+3=18 (hình lập phương đơn vị)





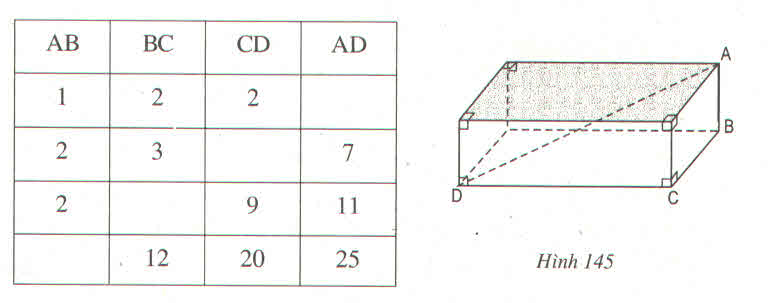
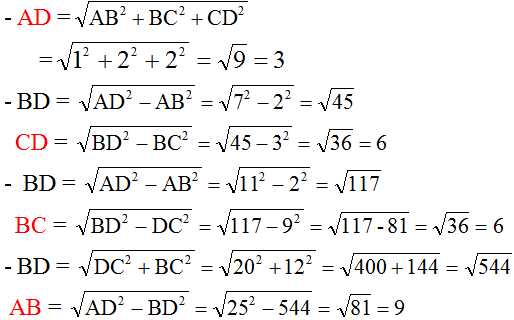 Ta có bảng sau:
Ta có bảng sau: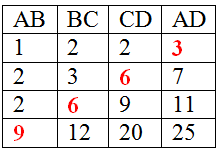
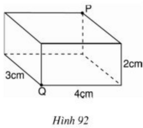

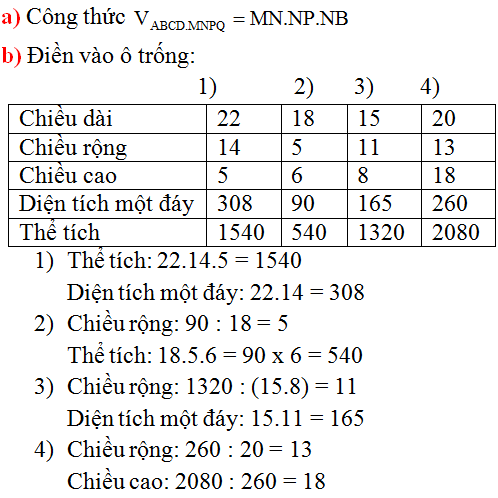
Trải 6 mặt của hình lập phương ABCD.A'B'C'D' . Để đi đường ngắn nhất từ M đến M' ( M' chính là trung điểm của A'D' trên mặt khai triển ) thì con kiến cần bò theo đoạn thẳng MM' . Trên chiếc hộp , đường đi ngắn nhất của con kiến là đường MNPQKZM ( dễ thấy N , P ,Q , K , Z lần lượt là trung điểm của DD' , CD , BC , BB' , A'B' )