Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B. Sau thời gian 2,5s thì vật dừng lại, sau đó tiếp tục chuyển động nhanh dần đều. Vận tốc của nó lúc t=5s là v = -10m/s

thời gian để xe đến C là
\(t=\frac{s_{BC}}{v}=\frac{50}{9}s\)
để gặp được xe mà đi với đoạn đường ngắn nhất thì người đó phải đi trên đoạn đường vuông gốc với BC
vậy vận tốc người đi bộ là
\(v=\frac{d}{t}=7,2\)m/s
sau 50/9s thì hai vật gặp nhau

A là gốc tọa độ, chiều dương từ A-B, gốc thời gian lúc hai vật bắt đầu chuyển động
x1=x0+vo.t+a.t2.0,5=10t-0,1t2
x2=x0+v0.t+a.t2.0,5=560-0,2t2
hai xe gặp nhau x1=x2\(\Rightarrow\)\(\left[{}\begin{matrix}t=40\left(n\right)\\t=-140\left(l\right)\end{matrix}\right.\)
vậy sau 40s hai xe gặp nhau
vị trí hai xe gặp nhau x1=x2=240m

\(\Rightarrow\left\{{}\begin{matrix}t1=\dfrac{S}{2+6}=\dfrac{3}{8}=0,375h\\t2=\dfrac{S}{3+5}=\dfrac{3}{8}=0,375h\end{matrix}\right.\)
\(\Rightarrow vtb=\dfrac{0,375\left(6+5\right)}{2.0,375}=5,5km/h\)
chon \(Ox\equiv AB,O\equiv A,\)(coi AB la khoang cach tu nha toi truong,)chieu(+) A->B
\(\Rightarrow\left\{{}\begin{matrix}x1=3t\\x2=3-2t\end{matrix}\right.\)\(\Rightarrow x1=x2\Rightarrow t=0,6h\)
\(\Rightarrow S=vtb.t=0,6.5,5=3,3km\)

Chọn B.
Gọi t là thời gian xe chạy từ A đến B.
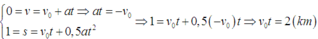
Quãng đường chó chạy được là: Scho = 4v0t = 8(km)

Gia tốc tức thời của chó ở vị trí ban đầu có thể được xác định bằng cách tính đạo hàm của vận tốc của chó theo thời gian tại vị trí ban đầu. Trong trường hợp này, vận tốc của chó không đổi, vì vậy gia tốc tức thời của chó ở vị trí ban đầu là 0.