Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
(a) Chu kì của dao động là T = 2 π ω = 2 s → ( a ) s a i
(b) Tốc độ cực đại của chất điểm là v m a x = ω . A = 18 , 8 c m / s → ( b ) đ ú n g
(c) Gia tốc của chất điểm có độ lớn cực đại là a m a x = ω 2 A = 59 , 2 c m / s 2 → ( c ) sai
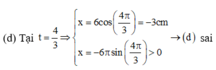
(e) Tốc độ trung bình của vật trong một chu kì dao động là v t b = 4 A T = 12 c m / s → ( e ) đ ú n g
(f) Tốc độ trung bình của vật trong một nửa chu kì dao động là v t b = 2 A 0 , 5 T = 12 c m / s → (f) sai
(g) Trong 0,25T vật có thể đi được quãng đường
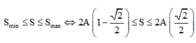
![]()

T=1s.
Trong thời gian 0,5s = T/2 vật đi quãng đường là 2.A = 2.8=16cm.

O A A' M N
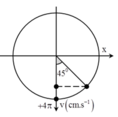
Giả sử M và N là 2 vị trí của chất điểm ở thười điểm t1 và t2.Dễ thấy t2 hơn t1 \(1/4\) chu kì nên \(\widehat{MON}=90^o\Rightarrow\widehat{AOM}+\widehat{A'ON}=90^o\)
Ta có:\(\cos^2\widehat{AOM}+\cos^2\widehat{A'ON}=cos^2\widehat{AOM}+sin^2\widehat{AOM}=1\)
\(\Rightarrow\dfrac{x_1^2}{A^2}+\dfrac{x_2^2}{A^2}=1\). Kết hợp với \(A^2=x_1^2+\dfrac{v_1^2}{\omega^2}=x_2^2+\dfrac{v_2^2}{\omega^2}\)
\(\Rightarrow x_1^2=\dfrac{v_2^2}{\omega^2}\Rightarrow v_2=\left|x_1\right|.\dfrac{2\pi}{T}=4\pi\)(\(cm/s\))
Do chọn \(OA\equiv Ox\) làm chiều dương nên \(v_2\) sẽ dương

+ Vận tốc cực đại của dao động amax = ωA = 4π cm/s.
+ Tại thời điểm t = 0,25 vật có vận tốc
v = 2 2 v m a x = 2 π 2 cm/s
Thời điểm t = 0 ứng với góc lùi Δφ = ωΔt = 0,25π.
Biểu diễn các vị trí tương ứng trên đường tròn. Ta thu được: φ 0 = - π 2 rad
+ Phương trình dao động của vật
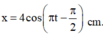
Đáp án C

Lần lượt kiểm tra từng phương án, ta thấy phương án đúng là \(v_{max} = \omega A = 6.\pi = 18,8 \ cm\)



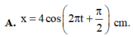
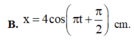
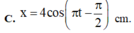
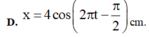
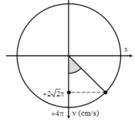

v=\(\frac{2A}{\frac{T}{2}}\)=2A\(\omega\)/\(\pi\)= 2*4*4\(\pi\)/\(\pi\)=32
Cảm ơn bạn Hue nhé, mình hơi gà mờ cái này.