
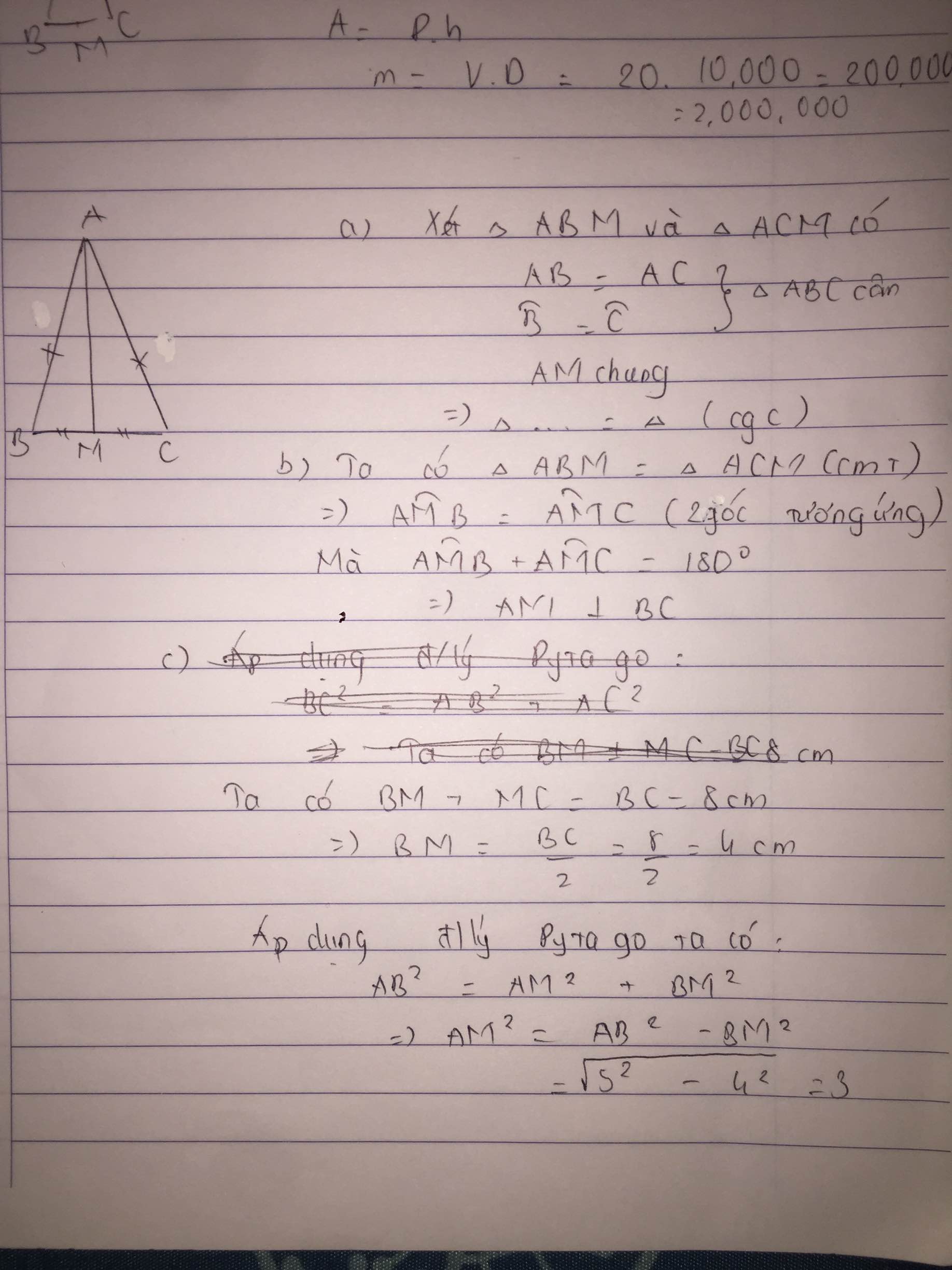
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

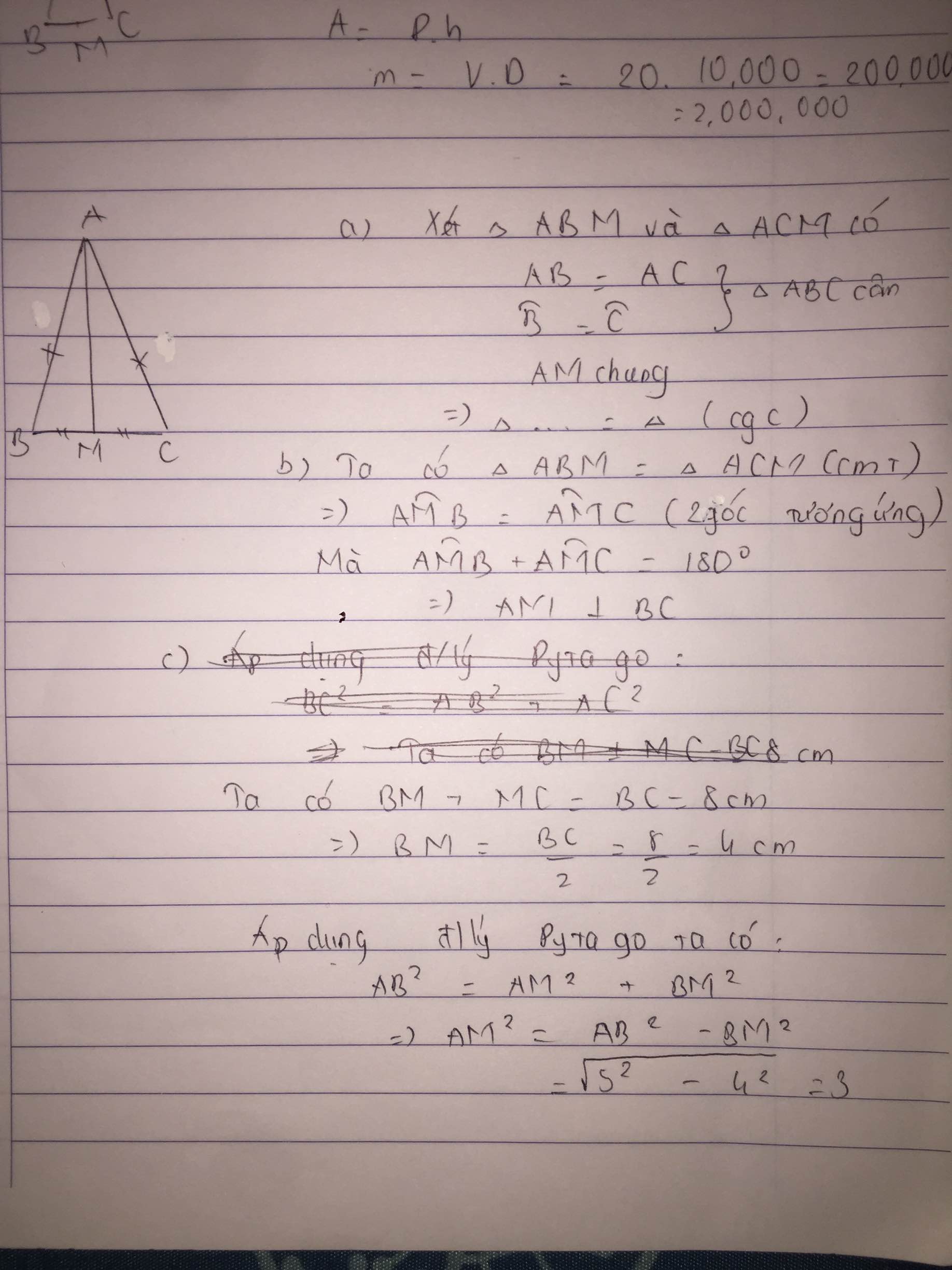

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM
A B C M
\(a,\) Xét \(\Delta ABM\) và \(\Delta ACM\) có:
\(AB=AC\) (giả thiết)
\(AM\) là cạnh chung
\(BM=CM\) (giả thiết)
\(\Rightarrow\Delta ABM=\Delta ACM\left(c.c.c\right)\)
\(b,\) Vì \(\Delta ABM=\Delta ACM\) (chứng minh câu \(a\))
\(\Rightarrow\widehat{BAM}=\widehat{CAM}\) (\(2\) góc tương ứng)
\(\Rightarrow AM\) là tia phân giác \(\widehat{BAC}\)
\(c,\) Vì \(\Delta ABC\) cân tại \(A\) (giả thiết)
Mà \(AM\) là tia phân giác \(\widehat{BAC}\) (chứng minh câu \(b\))
\(\Rightarrow AM\) là đường trung trực \(\Delta ABC\)
\(\Rightarrow AM\perp BC\) tại \(M\)

a) xét ΔABM và ΔACM có
góc B = góc C
AB = AC ( ΔABC cân tại A )
BM=CM ( tính chất các đường của Δ cân từ đỉnh )
=> ΔABM = ΔACM
b) xét ΔBME và ΔCMF có
góc B bằng góc C
BM=CM
=> ΔBME=ΔCMF ( cạnh huyền góc nhọn )
=> FM = EM
=> ΔEMF cân tại M
c) gọi giao của EF và AM là O
ta có BE = CF => AE=AF
=> ΔAEF cân tại A
ta có AM là tia phân giác của góc A
mà O nằm trên AM suy ra AO cũng là tia phân giác của góc A
ta lại có ΔAEF cân tại A
suy ra AO vuông góc với EF
suy ra AM vuông góc với EF
xét ΔAEF và ΔABC có
EF và BC đều cùng vuông góc với AM => EF // BC
a) Xét ΔABM và ΔACM có
AB=AC(ΔABC cân tại A)
AM chung
BM=CM(M là trung điểm của BC)
Do đó: ΔABM=ΔACM(c-c-c)
b) Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
BM=CM(M là trung điểm của BC)
\(\widehat{EBM}=\widehat{FCM}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔEMB=ΔFMC(Cạnh huyền-góc nhọn)
Suy ra: ME=MF(hai cạnh tương ứng)
Xét ΔEMF có ME=MF(cmt)
nên ΔEMF cân tại M(Định nghĩa tam giác cân)

xin gửi cho ng ae https://books.google.com.vn/books?id=owlmDwAAQBAJ&pg=PA58&lpg=PA58&dq=B%C3%A0i+to%C3%A1n+2:+tam+gi%C3%A1c+ABC+c%C3%A2n+t%E1%BA%A1i+A,+g%E1%BB%8Di+M+l%C3%A0+trung+%C4%91i%E1%BB%83m+c%E1%BB%A7a+BC+1,+Ch%E1%BB%A9ng+minh+AM+vu%C3%B4ng+g%C3%B3c+v+%E1%BB%9Bi+BC+AM+l%C3%A0+ph%C3%A2n+gi%C3%A1c+G%C3%B3c+BAC+2,+cho+BC+%3D6+cm,+AB+%3D10cm.+T%C3%ADnh+chu+vi+tam+gi%C3%A1c+ABM&source=bl&ots=PtijT9btGV&sig=ACfU3U1yMN80kRhao_IWaDOriwmgMEhUjQ&hl=vi&sa=X&ved=2ahUKEwi_lcqqqOrnAhXhwzgGHeABBkgQ6AEwAHoECAgQAQ#v=onepage&q=B%C3%A0i%20to%C3%A1n%202%3A%20tam%20gi%C3%A1c%20ABC%20c%C3%A2n%20t%E1%BA%A1i%20A%2C%20g%E1%BB%8Di%20M%20l%C3%A0%20trung%20%C4%91i%E1%BB%83m%20c%E1%BB%A7a%20BC%201%2C%20Ch%E1%BB%A9ng%20minh%20AM%20vu%C3%B4ng%20g%C3%B3c%20v%20%E1%BB%9Bi%20BC%20AM%20l%C3%A0%20ph%C3%A2n%20gi%C3%A1c%20G%C3%B3c%20BAC%202%2C%20cho%20BC%20%3D6%20cm%2C%20AB%20%3D10cm.%20T%C3%ADnh%20chu%20vi%20tam%20gi%C3%A1c%20ABM&f=false tại vì ngu toán hình nên dùng mạng giải cho ! xl ng ae !

A B C M 1 2 Q G
A) XÉT \(\Delta ABM\)VÀ\(\Delta ACM\)CÓ
\(AB=AC\left(GT\right)\)
\(\widehat{A_1}=\widehat{A_2}\left(GT\right)\)
AM LÀ CẠNH CHUNG
=>\(\Delta ABM\)=\(\Delta ACM\)( C-G-C)
TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ ĐƯỜNG CAO
=> AM LÀ ĐƯỜNG CAO CỦA \(\Delta ABC\)
\(\Rightarrow AM\perp BC\)
B) TRONG TAM GIÁC CÂN TIA PHÂN GIÁC CŨNG LÀ TRUNG TUYẾN
=> AM LÀ TRUNG TUYẾN THỨ NHẤT CỦA \(\Delta ABC\)
MÀ BG LÀ ĐƯỜNG TRUNG TUYẾN THỨ HAI CỦA \(\Delta ABC\)
HAI ĐƯỜNG TRUNG TUYẾN NÀY CẮT NHAU TẠI G
\(\Rightarrow G\)LÀ TRỌNG TÂM CỦA \(\Delta ABC\)