Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Vẽ vecto \(\overrightarrow {AB} \) là vecto vận tốc của máy bay, \(\overrightarrow {AD} \) là vecto vận tốc của gió.
Khi đó vecto vận tốc mới của máy bay là \(\overrightarrow {AB} + \overrightarrow {AD} \)
Dựng hình bình hành ABCD. Ta có: \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \)
Áp dụng định lí cosin trong tam giác ABC, ta có:
\(A{C^2} = A{B^2} + B{C^2} - 2.AB.BC.\cos B\)
Mà AB = 700, BC = AD = 40, \(\widehat B = {135^o}\)
\(\begin{array}{l} \Rightarrow A{C^2} = {700^2} + {40^2} - 2.700.40.\cos {135^o} \approx 531197,98\\ \Leftrightarrow AC \approx 728,83\end{array}\)
Vậy tốc độ mới của máy bay là 728,83 km/h.

a) Vận tốc 240 km/h nên \(\left| {\overrightarrow v } \right| = AC = 240\)
Áp dụng các tính chất trong tam giác vuông ta có
\(AB = DC = AC.\cos (\widehat {CAB}) = 240.\cos (30^\circ ) = 120{\sqrt 3 }\)
\(AD = BC = AC.\sin (\widehat {CAB}) = 240.\sin (30^\circ ) = 120\)
b) Xem A là gốc tọa độ nên ta có \(\overrightarrow {AB} = 120\overrightarrow i ,\overrightarrow {AD} = 120{\sqrt 3 }\overrightarrow j ,\overrightarrow v = \overrightarrow {AC} = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
c)
Ta có \(\overrightarrow v = 120\overrightarrow i + 120{\sqrt 3 }\overrightarrow j \)
Vậy tọa độ của vectơ \(\overrightarrow v \) là \(\left( {120;120{\sqrt 3 }} \right)\)

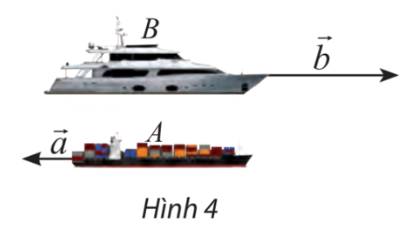
Ta thấy hai hướng đông và tây là ngược nhau và tỉ số độ dài \(\frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{50}}{{20}} = \frac{5}{2}\)
\( \Rightarrow \overrightarrow b = - \frac{5}{2}\overrightarrow a \)


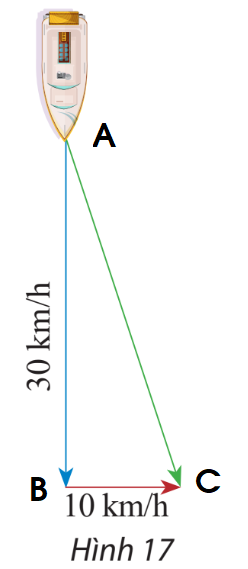
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Gọi vecto vận tốc của tàu là \(\overrightarrow {AB} \), vecto vận tốc của dòng nước là vecto \(\overrightarrow {BC} \)
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).
Ta có vecto tổng là \(\overrightarrow F = \overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Độ dài vecto tổng là \(\left| {\overrightarrow F } \right| = \left| {\overrightarrow {AC} } \right| = AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{30}^2} + {{10}^2}} = 10\sqrt {10} \)(km/h)
Vậy độ dài vecto tổng là \(10\sqrt {10} \)(km/h).

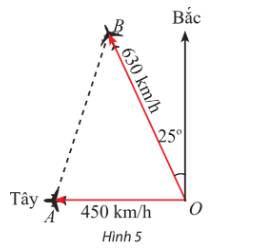
Ta có: \(\widehat {BOA} = {90^o} - {25^o} = {65^o}.\)
Sau 90 phút = 1,5 giờ:
Máy bay thứ nhất đi được quãng đường (OA) là: \(450.1,5 = 675\;(km)\)
Máy bay thứ hai đi được quãng đường (OB) là: \(630.1,5 = 945\;(km)\)
Áp dụng định lí cosin trong tam giác OAB, ta có:
\(\begin{array}{l}A{B^2} = O{A^2} + O{B^2} - 2OA.OB\cos O\\ \Leftrightarrow A{B^2} = {675^2} + {945^2} - 2.675.945\cos {65^o}\\ \Rightarrow AB \approx 900\end{array}\)
Vậy sau 90 phút, hai máy bay cách nhau khoảng 900 km.

Gọi vectơ chỉ vận tốc của máy bay là vectơ \(\overrightarrow {AB} \) và vectơ chỉ vận tốc của gió là vectơ \(\overrightarrow {BC} \).
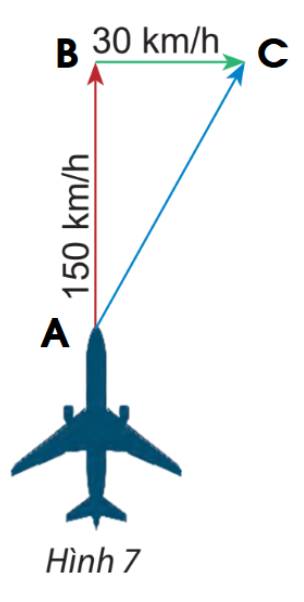
Ta có: \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \)
Áp dụng định lý Pitago ta có:
\(AC = \sqrt {A{B^2} + B{C^2}} = \sqrt {{{150}^2} + {{30}^2}} = 30\sqrt {26} \)
Vậy độ dài vectơ tổng của hai vectơ nói trên là \(30\sqrt {26} \) km/h

Từ giả thiết ta có:
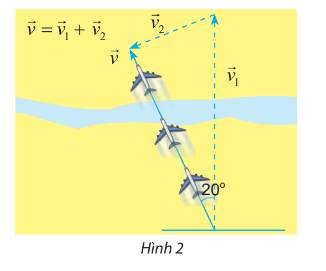
+) Vectơ tương ứng với vận tốc máy bay là vectơ \(\overrightarrow {{v_1}} \)
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ \(\overrightarrow v \)
+) Vectơ tương ứng với vận tốc gió là vectơ \(\overrightarrow {{v_2}} \)
Ta có : \(\left| {\overrightarrow {{v_1}} } \right| = 45;\left| {\overrightarrow v } \right| = 38;\left( {\overrightarrow {{v_1}} ,\overrightarrow v } \right) = 20^\circ \)
Áp dụng định lý cosin ta có:
\(\left| {\overrightarrow {{v_2}} } \right| = \sqrt {{{\left| {\overrightarrow v } \right|}^2} + {{\left| {\overrightarrow {{v_1}} } \right|}^2} - 2\left| {\overrightarrow v } \right|.\left| {\overrightarrow {{v_1}} } \right|.\cos \left( {\overrightarrow v ,\overrightarrow {{v_1}} } \right)} \)
\( = \sqrt {{{38}^2} + {{45}^2} - 2.38.45.\cos 20^\circ } \simeq 16\) (m/s)
Vậy tốc độ của gió gần bằng 16 m/s

Tọa độ của vecto \(\overrightarrow {OM} \) là tọa độ của điểm M (trong đó O là gốc tọa độ)

Đáp án: C
Ta có một năm có 365 ngày, một ngày có 24 giờ, một giờ có 60 phút và một phút có 60 giây.
Vậy một năm có 24.365.60.60 = 31536000 giây.
Vì vận tốc ánh sáng là 300 nghìn km/s nên trong vòng một năm nó đi được 31536000.300 = 9,4608.109 km.
0 km vì 1 vật có khối lượng ko thể đạt tới vận tốc ánh sáng, và chắc chắc ko có nhà khoa học nào lại nghiên cứu 1 máy bay vs tốc độ 7 lần vận tốc ánh sáng
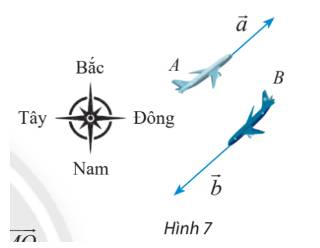




Vecto \(\overrightarrow a ,\;\overrightarrow b \) là vecto vận tốc của máy bay A và máy bay b.
Do đó \(\left| {\overrightarrow a } \right|,\;\left| {\overrightarrow b } \right|\) lần lượt là độ lớn của vecto vận tốc tương ứng.
Ta có: \(\left| {\overrightarrow a } \right| = 600,\;\left| {\overrightarrow b } \right| = 800\)
\( \Rightarrow \frac{{\left| {\overrightarrow b } \right|}}{{\left| {\overrightarrow a } \right|}} = \frac{{800}}{{600}} = \frac{4}{3}\)
Hai hướng Đông Bắc và Tây Nam là ngược nhau, do đó \(\overrightarrow b = - \frac{4}{3}\overrightarrow a \)