Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi A: “Học sinh thích môn Bóng đá”
B: “Học sinh thích môn Bóng bàn”
Do đó ta có \(P\left( A \right) = \frac{{19}}{{30}},P\left( B \right) = \frac{{17}}{{30}},P\left( {AB} \right) = \frac{{15}}{{30}}\)
Theo công thức cộng xác suất
\(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right) - P\left( {AB} \right) = \frac{{19}}{{30}} + \frac{{17}}{{30}} - \frac{{15}}{{30}} = \frac{{21}}{{30}} = \frac{7}{{10}}\)
Vậy xác suất để chọn được học sinh thích ít nhất một trong hai môn Bóng đá hoặc Bóng bàn là \(\frac{7}{{10}}\)

Gọi B là tập hợp “học sinh thích học Lý”
Gọi C là tập hợp ” học sinh thích học ít nhất một môn “
Ta có n(C) = n( A ∪ B) = n(A) + n(B) – n(A ∩ B) = 30 + 25 – 10 = 45
Vậy xác suất để được học sinh này thích học ít nhất là một môn Toán hoặc Lý là: 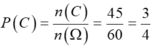
Chọn B.

a) \(P\left( A \right)\) là tỉ lệ học sinh học khá môn Ngữ văn trong tổng số học sinh của trường X
\(P\left( B \right)\) là tỉ lệ học sinh học khá môn Toán trong tổng số học sinh của trường X
\(P\left( {AB} \right)\) là tỉ lệ học sinh học khá cả hai môn Ngữ văn và Toán trong tổng số học sinh của trường X
\(P\left( {A \cup B} \right)\) là tỉ lệ học sinh học khá ít nhất một trong hai môn Ngữ văn và Toán trong tổng số học sinh của trường X
b) Ta không áp dụng được công thức \(P\left( {A \cup B} \right) = P\left( A \right) + P\left( B \right)\) vì hai biến cố A và B không độc lập với nhau do học sinh học khá môn Ngữ Văn có thể cũng học khá môn Toán (7% học sinh học khá cả hai môn Ngữ văn và Toán)

a) A = {Dung, Long, Cường, Trang}
B = {Lan, Hương, Phúc, Cường, Trang}
C = {Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b) A ∪ B = {Dung, Long, Cường, Trang, Lan, Hương, Phúc}
a: A={Dung, Long, Cường, Trang}
B={Lan, Hương, Phúc, Cường, Trang}
C={Dung, Long, Lan, Hương, Phúc, Cường, Trang}
b: A hợp B={Dung,Long,Cường,Trang,Phúc,Hương,Lan}

Kí hiệu A 1 , A 2 , A 3 lần lượt là các biến cố: Học sinh được chọn từ khối I trượt Toán, Lí, Hoá: B 1 , B 2 , B 3 lần lượt là các biến cố : Học sinh được chọn từ khối II trượt Toán, Lí, Hoá. Rõ ràng với mọi (i,j), các biến cố A i và B i độc lập.
a) 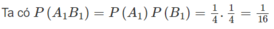
b) Xác suất cần tính là
P ( ( A 1 ∪ A 2 ∪ A 2 ) ∩ ( B 1 ∪ B 2 ∪ B 3 ) ) = P ( A 1 ∪ A 2 ∪ A 2 ) . P ( B 1 ∪ B 2 ∪ B 3 ) = 1 / 2 . 1 / 2 = 1 / 4
c) Đặt A = A 1 ∪ A 2 ∪ A 3 , B = B 1 ∪ B 2 ∪ B 3
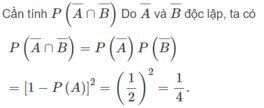
d) Cần tính P(A ∪ B)
Ta có
P(A ∪ B) = P(A) + P(B) − P(AB)
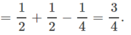

Cặp biến cố E và F không xung khắc vì nếu học sinh được chọn thích môn Bóng đá thì cả E và F có thể xảy ra vì có 2 bạn thích cả hai môn Bóng đá và Cầu lông.
Vì có 2 bạn cùng thích bóng đá và cầu lông
nên hai biến cố E và F không xung khắc

Đáp án A
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố“3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”.
Số phần tử của biến cố A là
![]()
Vậy xác suất cần tìm là
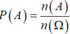
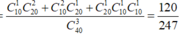

Chọn B
Số phần tử của không gian mẫu là ![]()
- Gọi A là biến cố “3 học sinh được chọn luôn có học sinh chọn môn Vật lý và học sinh chọn môn Hóa học”
- Số phần tử của biến cố A là
![]()
Vậy xác suất để xảy ra biến cố A là
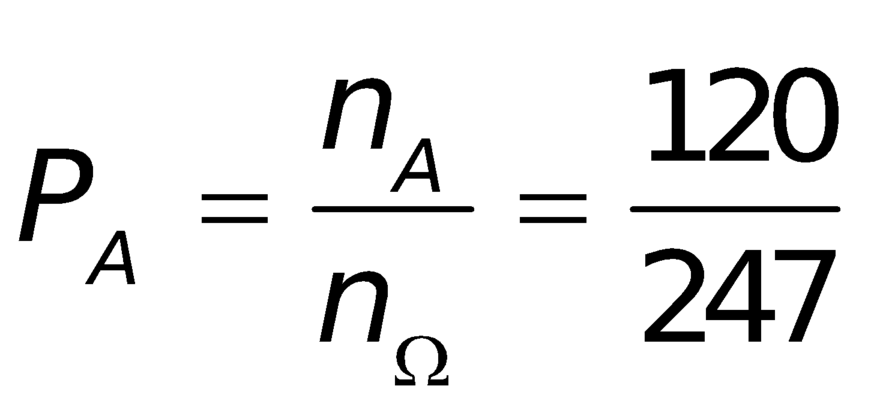 .
.

Trong mỗi khối, XS hs trượt Toán là 0,25; trượt Lý là 0,15; trượt cả 2 môn là 0,1; trượt đúng 1 môn là 0,2; chỉ trượt Toán là 0,15; chỉ trượt Lý là 0,05; trượt ít nhất 1 môn là 0,3; ko trượt môn nào là 0,7
a) P = 0,25^2 = 0,0625
b) Câu này đề chưa rõ ràng, có nhiều cách hiểu
..1) 2 hs đó đều bị trượt ít nhất 1 môn
..2) 2 hs đó cùng bị trượt trong 1 môn nào đó (còn môn kia không trượt)
..3) 2 hs đó cùng bị trượt trong 1 môn nào đó (còn môn kia có thể trượt hoặc không)
..Nếu hiểu theo cách 1 thì P = 0,3^2 = 0,09
..Nếu hiểu theo cách 2 thì P = 0,15^2 + 0,05^2 = 0,025
..Nếu hiểu theo cách 3 thì P = 0,25^2 + 0,15^2 - 0,1^2 = 0,075
c) P = 0,7^2 = 0,49
d) Trường hợp này là biến cố đối lập với biến cố c
..P = 1 - 0,7^2 = 0,51

Có 2 bạn giỏi văn , 7 bạn giỏi toán, 3 bạn giỏi cả 2 môn
Có 2C1.7C1 =14 ( cách )
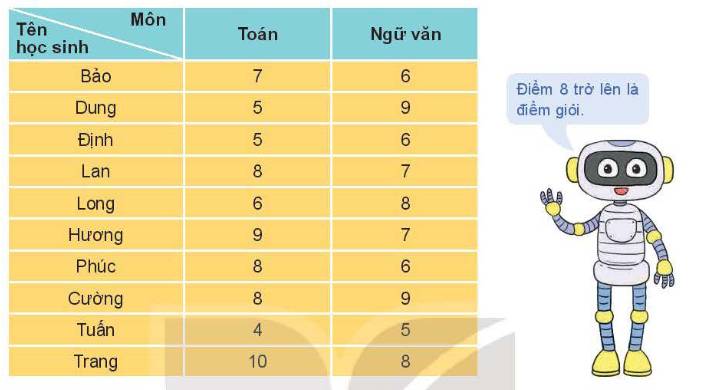
a) Số học sinh thích học ít nhất một trong 2 môn là \(38-3=35\)
\(\Rightarrow P=\dfrac{35}{38}\)
b) Gọi M, L lần lượt là tập hợp các học sinh thích học toán và văn.
\(\Rightarrow\left|M\cap L\right|=\left|M\right|+\left|L\right|-\left|M\cup L\right|\) \(=25+20-35=10\)
\(\Rightarrow P=\dfrac{10}{38}=\dfrac{5}{19}\)