Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(n\left(\Omega\right)=C^4_{10}=210\)
A: "Không chọn được hai chiếc nào tạo thành một đôi".
\(\overline{A}\): "Chọn được ít nhất hai chiếc tạo thành một đôi".
\(n\left(\overline{A}\right)=C^1_5\cdot C_8^2=140\).
\(n\left(A\right)=210-140=70\).
\(P\left(A\right)=\dfrac{70}{210}=\dfrac{1}{3}\).

Phép thử T được xét là: "Lấy ngẫu nhiên 2 chiếc giày từ 4 đôi giày có cỡ khác nhau".
Mỗi một kết quả có thể là một tổ hợp chập 2 của 8 chiếc giày. Do đó số các kết quả có thể có thể có của phép thử T là n(Ω) = C28 = = 28.
Vì lấy ngẫu nhiên, nên các kết quả có thể có của phép thử T là đồng khả năng. Gọi A là biến cố: "Lấy được hai chiếc giày tạo thành một đôi". Mỗi một kết quả có thể có thuận lợi cho A là một đôi giày trong 4 đôi giày đã cho. Do đó số các kết quả có thể có thuận lợi cho A là n(A) = 4. Suy ra P(A) = =
.

Không gian mẫu là kết quả của việc chọn ngẫu nhiên 2 chiếc giày trong số 8 chiếc giày.
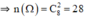
A: “ Chọn được 2 chiếc tạo thành một đôi”
⇒ n(A) = 4 (Vì có 4 đôi).

Èo toàn bài khó nhằn :( Thôi làm được mỗi câu 2, câu 1 thì...dẹp đi
\(n\left(\Omega\right)=9.9.8.7.6.5\)
Số lẻ vậy thì f={1;3;5;7;9}
Nhưng nếu f=1 thì ko tồn tại a thỏa mãn a<f do a khác 0
f=3 cũng ko thỏa mãn do nếu a=1; b=2; nhưng ko tồn tại c thỏa mãn :v
f=5 tương tự, ko tồn tại e thỏa mãn
=> f={7;9}
Nếu f=7 thì (a,b,c,d,e)={1;2;3;4;5;6} và chỉ có duy nhất 1 cách sắp xếp \(\Rightarrow C^5_6\left(cach\right)\)
Nếu f=9 thì (a,b,c,d,e)={1;2;3;4;5;6;7;8} và chỉ có duy nhất một cách xếp \(\Rightarrow C^5_8\left(cach\right)\)
\(\Rightarrow n\left(A\right)=C^5_6+C^5_8\) \(\Rightarrow p\left(A\right)=\dfrac{n\left(A\right)}{n\left(\Omega\right)}=...\)
Gọi A là số tự nhiên có 8 chữ số a1a2a3a4a5a6a7a8 chia hết cho 1111
9999a1a2a3a4 + a1a2a3a4+a5a6a7a8 để A chia hết cho 1111 thì a1a2a3a4+a5a6a7a8 chia hết cho 1111
1000(a1 + a5) + 100(a2 + a6) + 10(a3 + a7) + (a4+ a8) (1) chia hết cho 1111
đặt (a1 + a5) = x
(a2 + a6) = y
(a3 + a7) = z
(a4+ a8) = t
3<=x<=15
xét đk
suy ra x = 9
suy ra x=y=z=t= 9
suy ra x+y+z+t=36 suy ra t= 36-x-y-z
thế vào (1) suy ra
999(a1 + a5) + 99(a2 + a6) + 9(a3 + a7) =36
hoán vị .......
suy ra có 3840 số

Chọn C
Lời giải. Ta có n ( Ω ) = C 10 3 n ( A ¯ ) = C 8 3
⇒ P = 1 - C 8 3 C 10 3 = 8 15
Gọi A là biến cố " 3 chữ số trên 3 chiếc thẻ được lấy ra có thể ghép thành một số chia hết cho 5".
→ biến cố A ¯ " 3 thẻ lấy ra không có thẻ mang chữ số 0 và cũng không có thẻ mang chữ số 5"
nên có
C
8
3
cách



ta có : \(n\left(\Omega\right)=C^6_{20}=38760\)
a) Gọi A : " chọn ra 6 chiếc gang tay mà không tạo thành đôi nào "
=> n(A) = \(\left(C^6_{10}+C^5_{10}.C^1_5+C^4_{10}.C^2_6+C^3_{10}.C^3_7+C^2_{10}.C^4_8+C^1_{10}.C^5_9+C^6_{10}\right)=13440\)
=> P(A)= 13440 / 38760 = 112/323
" Lưu ý : ta phải bân biệt gang tay trái và gang tay phải ... tự đọc rồi tìm hiểu xem tại sao lại vậy .. ko hiểu thì hỏi lại t giải thích cho :) "
b) Gọi B :" 6 chiếc lấy ra trong đó có 1 đôi "
=> n(B) = \(C^1_{10}.C^4_9+C^1_{10}.C^3_9.C^1_6+C^1_{10}.C^2_9.C^2_7+C^1_{10}.C^1_9.C^3_8+C^1_{10}.C^4_9=20160\)
=>P(A) = 20160 / 38760 =168/323