Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình bậc hai có dạng: a\(x^2\) + b\(x\) + c
Bước 1: Đưa nó về bình phương của một tổng hoặc một hiệu cộng với một số nào đó. nếu a > 0 thì em sẽ tìm giá trị nhỏ nhất; nếu a < 0 thì em sẽ tìm giá trị lớn nhất
Bước 2: lập luận chỉ ra giá trị lớn nhất hoặc nhỏ nhất
Bước 3: kết luận
Giải:
A = 3\(x^2\) - 5\(x\) + 3 Vì a = 3 > 0 vậy biểu thức A chỉ tồn tại giá trị nhỏ nhất
A = 3\(x^2\) - 5\(x\) + 3
A = 3.(\(x\)2 - 2.\(x\).\(\dfrac{5}{6}\) + \(\dfrac{25}{36}\)) + \(\dfrac{11}{12}\)
A = 3.(\(x\) - \(\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\)
Vì (\(x-\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x\) - \(\dfrac{5}{6}\))2 ≥ 0 ⇒ 3.(\(x-\dfrac{5}{6}\))2 + \(\dfrac{11}{12}\) ≥ \(\dfrac{11}{12}\)
Amin = \(\dfrac{11}{12}\) ⇔ \(x\) = \(\dfrac{5}{6}\)

Trả lời
2002 x 1006
= ( 1504 + 498 ) x ( 1504 - 498 )
= 15042 - 4982
= 2014012
198 x 202
= ( 200 - 2 ) x ( 200 + 2 )
= 2022 - 22
= 40800

Dễ lắm( -.-)
Đầu tiên học 3 hằng đẳng thức viết vào tập khoảng 4,5 lần nếu thuộc rồi thì chuyển qua 3 cái khác đến hết 7 hằng đẳng thức thì xong:-)

một bài bđt khó nha cho a,b,c là các số dương thỏa mãn a+b+c=3. Tìm giá trị nhỏ nhất của biểu thức sau:
P=1/1+a^2 +1/1+b^2 +1/1+c^2

\(A=x^2-6x+10=\left(x-3\right)^2+1\ge1\)
\(\Rightarrow A_{min}=1\Leftrightarrow x=3\)
\(B=4x^2-4x+25=\left(2x-1\right)^2+24\ge24\)
\(\Rightarrow B_{min}=24\Leftrightarrow x=\frac{1}{2}\)
\(C=3x^2+9x+12=3\left(x+\frac{3}{2}\right)^2+\frac{21}{4}\ge\frac{21}{4}\)
\(\Rightarrow C_{min}=\frac{21}{4}\Leftrightarrow x=\frac{-3}{2}\)

Học hằng đẳng thức chưa vậy em :3
(x+2y-3)2 - 4(x+2y-3)+4
= ((x+2y-3)2 - 2.2(x+2y-3)+2^2
=((x+2y-3)-2)^2
Cậu hok hằng đẳng thức chưa vậy :))
\(\left(x+2y-3\right)^2-4\left(x+2y-3\right)+4\)
\(=\left(x+2y-3\right)^2-2.\left(x+2y-3\right).2+2^2\)
\(=\left[\left(x+2y-3\right)-2\right]^2\)
\(=\left(x+2y-5\right)^2\)

\(P=2x^2+x+1\)
\(P=\left(\sqrt{2}.x\right)^2+2.\sqrt{2}.\frac{1}{2}x+\frac{1}{2}-\frac{1}{2}+1\)
\(P=\left(\sqrt{2}.x+\sqrt{\frac{1}{2}}\right)^2-\left(\frac{1}{2}-1\right)\)
\(P=\left(x\sqrt{2}+\sqrt{\frac{1}{2}}\right)^2-\left(-\frac{1}{2}\right)\)
\(P=\left(x\sqrt{2}+\sqrt{\frac{1}{2}}\right)^2-\left(-\sqrt{\frac{1}{2}}\right)^2\)
\(P=\left(x\sqrt{2}+\sqrt{\frac{1}{2}}-\sqrt{\frac{1}{2}}\right)\left(x\sqrt{2}+\sqrt{\frac{1}{2}}-\sqrt{\frac{1}{2}}\right)\)
\(P=\left(x\sqrt{2}\right)\left(x\sqrt{2}\right)\)
\(P=\left(x\sqrt{2}\right)^2\)
\(P=2x^2\)
Vd : \(x^2+6x+10\)
Ta có : 10 không căn được
Mà : \(x^2+2.x.3+3^2\)
Nhưng 32 chỉ là 9 nên ta cộng thêm 1 ở vế sau
\(\left(x^2+2.x.3+3^2\right)+1\)
\(\left(x+3\right)^2+1\)
Dư 1 ở ngoài :
Vì \(\left(x+3\right)^2\ge0\)
=> \(\left(x+3\right)^2+1\ge1\)
=> GTNN là 1
Khi ( x + 3 ) = 0
x = -3
Khi
Giải
Ta có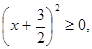 nên
nên 
Vậy: f(x) đạt GTNN bằng khi
khi 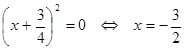
Ta có nên
nên 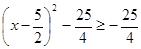
Vậy: g(x) đạt GTNN bằng khi
khi 