Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 2:
c/ DO M thuộc \(\Delta\) nên tọa độ M có dạng \(M\left(a;\frac{1-3a}{2}\right)\)
Áp dụng công thức khoảng cách:
\(\frac{\left|5a-\frac{3\left(1-3a\right)}{2}+2\right|}{\sqrt{5^2+3^2}}=5\)
\(\Leftrightarrow\left|13a+1\right|=10\sqrt{34}\)
\(\Leftrightarrow\left[{}\begin{matrix}13a+1=10\sqrt{34}\\13a+1=-10\sqrt{34}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}a=\frac{-1+10\sqrt{34}}{13}\\a=\frac{-1-10\sqrt{34}}{13}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(\frac{-1+10\sqrt{34}}{13};\frac{8-15\sqrt{34}}{13}\right)\\M\left(\frac{-1-10\sqrt{34}}{13};\frac{8+15\sqrt{34}}{13}\right)\end{matrix}\right.\)
d/ Chẳng hiểu đề câu d là gì luôn? Cái gì bằng 2 lần khoảng cách từ N đến d bạn
Câu 2:
a/ Khoảng cách:
\(d\left(A;\Delta\right)=\frac{\left|3.5+2.4-1\right|}{\sqrt{3^2+2^2}}=\frac{22\sqrt{13}}{13}\)
b/ Gọi \(M\left(x;y\right)\) là 1 điểm thuộc đường phân giác
\(\Rightarrow d\left(M;\Delta\right)=d\left(M;d\right)\)
\(\Rightarrow\frac{\left|3x+2y-1\right|}{\sqrt{3^2+2^2}}=\frac{\left|5x-3y+2\right|}{\sqrt{5^2+3^2}}\)
\(\Leftrightarrow\sqrt{34}\left|3x+2y-1\right|=\sqrt{13}\left|5x-3y+2\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{34}\left(3x+2y-1\right)=\sqrt{13}\left(5x-3y+2\right)\\\sqrt{34}\left(3x+2y-1\right)=-\sqrt{13}\left(5x-3y+2\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left(3\sqrt{34}-5\sqrt{13}\right)x+\left(2\sqrt{34}+3\sqrt{13}\right)y-\sqrt{34}-2\sqrt{13}=0\\\left(3\sqrt{34}+5\sqrt{13}\right)x+\left(2\sqrt{34}-3\sqrt{13}\right)y-\sqrt{34}+2\sqrt{13}=0\end{matrix}\right.\)

9. Cho đg thẳng d 3x +4y -5=0 và 2 điểm A(1;3) , B(2;m). Định m để A và B nằm cùng phía đối với d.
Hai điểm A và B nằm cùng phía với (d)
\(\Leftrightarrow\)(3.1+4.3-5).(3.2+4.m-5)>0
\(10\left(6+4m-5\right)>0\)
\(60+40m-50>0\Rightarrow m>-\frac{1}{4}\)
10. Cho tam giác ABC với A(1;3) , B(-2;4) ,C(-1;5) và đg thẳng d : 2x -3y +6=0. Đg thẳng d cắt cạnh nào của tg ABC?
(bạn xem lại đề)
11. Khoảng cách từ điểm M (1;-1) đến đg thẳng denta 3x -4y -17=0 là:
\(d_{\left(M,\Delta\right)}=\frac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}=\frac{\left|3.1-4.\left(-1\right)-17\right|}{\sqrt{3^2+\left(-4\right)^2}}\)\(=2\)
Câu 12,13 tương tự vậy
14. Khoảng cách từ điểm M(0;2) đến đg thẳng denta x =1 +3t ; y = 2+4t là:
\(\Delta:\left\{{}\begin{matrix}x=1+3t\\y=2+4t\end{matrix}\right.\)
PTTQ của delta:\(4x-3y+2=0\)
áp dụng ct:
\(d_{\left(M,\Delta\right)}=\frac{\left|ax_0+by_0+c\right|}{\sqrt{a^2+b^2}}=\frac{4}{5}\)
( bạn xem lại đáp án)
16. Tính diện tích tg ABC biết A(-2;1) , B(1;2) , C (2;-4)
sABC= 5,5

Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=\frac{\left|3.1-4\left(-1\right)-17\right|}{\sqrt{3^2+4^2}}=\frac{10}{5}=2\)

Lời giải:
Khoảng cách từ điểm $N$ đến $d$ bạn chỉ cần áp dụng công thức thôi:
\(d(N,d)=\frac{|3.2+4(-1)-10|}{\sqrt{3^2+4^2}}=\frac{8}{5}\)
Ghi nhớ: Đường thẳng \( ax+by+c=0\) thì khoảng cách từ \(M(x_0;y_0)\) đến đường thẳng đã cho là:
\(d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}}\)
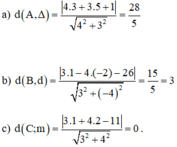

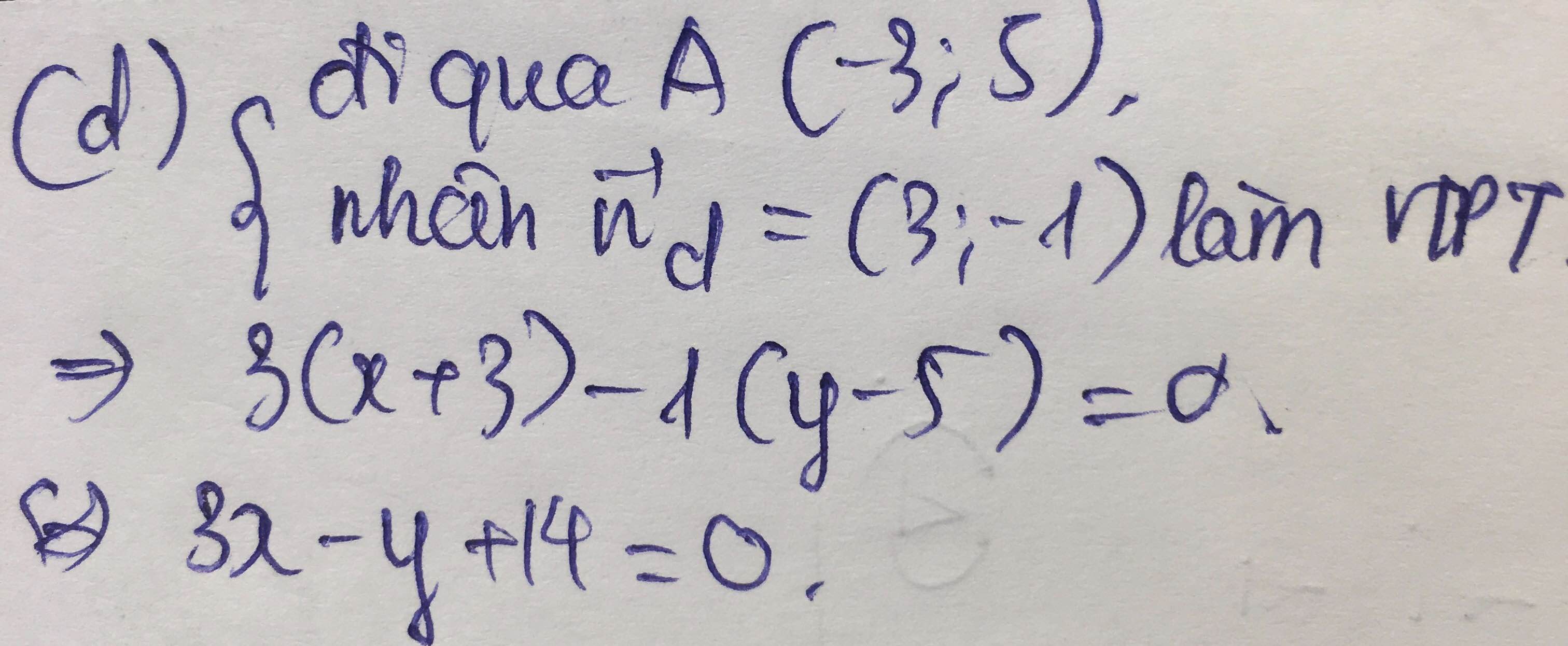

Chọn B.
Vậy khoảng cách từ điểm M(1;-1) đến đường thẳng Δ: 3x + y + 4 = 0 là