Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hai mặt phẳng song song (α) và (β) nên có 1 đường thằng a ∈ (α) và a // (β)
⇒ Khoảng cách giữa đường thẳng a và mặt phẳng (β) là bé nhất so với khoảng cách từ một điểm bất kì thuộc a tới một điểm bất kì thuộc mặt phẳng (β).
Vậy khoảng cách giữa hai mặt phẳng song song (α) và (β) là nhỏ nhất trong các khoảng cách từ một điểm bất kì của mặt phẳng này tới một điểm bất kì của mặt phẳng kia.

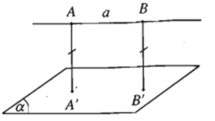
Lấy điểm A ∈ a, A’ là hình chiếu của A trên mặt phẳng (α) ⇒ AA’ = khoảng cách từ A đến mặt phẳng (α)
Mà khoảng cách từ A đến mặt phẳng (α) là bé nhất so với các khoảng cách từ A tới một điểm bất kì của mặt phẳng (α).
Vậy khoảng cách giữa đường thẳng a và mặt phẳng (α) là bé nhất so với khoảng cách từ một điểm bất kì thuộc a tới một điểm bất kì thuộc mặt phẳng (α).

Đáp án D.
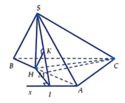
Kẻ Ax//BC, HI ⊥ Ax; HK ⊥ SI.
Gọi M là trung điểm của AB
![]()
![]()
Ta có AI ⊥ (SHI)=> AI ⊥ HK=> HK ⊥ (SAI)=>d(H,(Sax)) = HK
Góc giữa SC và (ABC) là góc S C H ^ = 60 0
Ta có:
![]()
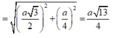
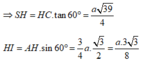
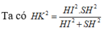
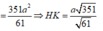
![]()
![]()

Đáp án B.
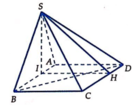
Ta có AD//BC, ![]() => AD//(SBC)
=> AD//(SBC)
=> d(AD;SC) = d(AD;(SBC)) = d(D;(SBC)).
Qua I kẻ đường thẳng song song với AD, cắt CD tại H.
Suy ra IH ⊥ CD
Từ CD ⊥ IH, CD ⊥ SI=> CD ⊥ (SIH)=> CD ⊥ SH
Suy ra ![]()
![]()
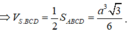
Lại có
![]()
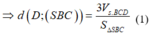
Từ ![]()
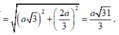
![]()
![]()
Suy ra
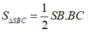
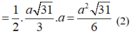
Từ (1) và (2), suy ra
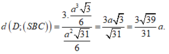
Vậy
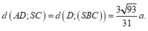

a) Để tính khoảng cách từ điểm O đến đường thẳng Δ không đi qua O, ta xác định mặt phẳng (O; Δ) và trong mặt phẳng này kẻ OH ⊥ Δ. Độ dài OH chính là khoảng cách từ O đến Δ.
b) Để tính khoảng cách giữa đường thẳng a và mp(α) song song với a, ta lấy một điểm M bất kì thuộc đường thẳng a. Gọi N là hình chiếu của M trên mp(α) . Khoảng cách MN từ điểm M đến mp(α) chính là khoảng cách giữa đường thẳng a và mp(α) song song với a.
c) Để tính khoảng cách giữa hai mp(P) và (P’) song song với nhau, ta lấy một điểm M thuộc (P). Gọi H là hình chiếu của M lên (P’). Khi đó, MH chính là khoảng cách giữa hai mp (P) và (P’).

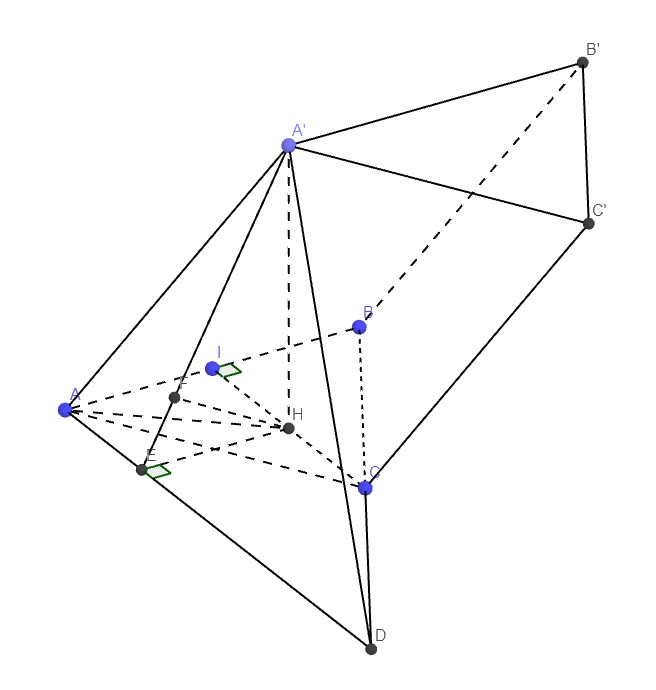
Qua A kẻ đường thẳng song song CI cắt BC kéo dài tại D
\(\Rightarrow CI||\left(A'AD\right)\Rightarrow d\left(A'A;CI\right)=d\left(CI;\left(A'AD\right)\right)=d\left(H;\left(A'AD\right)\right)\)
Từ H kẻ \(HE\perp AD\), từ H kẻ \(HF\perp A'E\)
\(\Rightarrow HF\perp\left(A'AD\right)\Rightarrow HF=d\left(H;\left(A'AD\right)\right)\)
Tứ giác AIHE là hình chữ nhật (3 góc vuông) \(\Rightarrow HE=AI=\dfrac{a}{2}\)
\(A'H\perp\left(ABC\right)\Rightarrow\widehat{A'AH}\) là góc giữa \(A'A\) là (ABC)
\(\Rightarrow\widehat{A'AH}=45^0\)
\(CI=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều) \(\Rightarrow IH=\dfrac{1}{2}CI=\dfrac{a\sqrt{3}}{4}\)
\(\Rightarrow AH=\sqrt{AI^2+IH^2}=\dfrac{a\sqrt{7}}{4}\)
\(\Rightarrow A'H=AH.tan45^0=\dfrac{a\sqrt{7}}{4}\)
Hệ thức lượng:
\(HF=\dfrac{HE.A'H}{\sqrt{HE^2+A'H^2}}=\dfrac{a\sqrt{77}}{22}\)

a) Để tính khoảng cách từ điểm O đến đường thẳng Δ không đi qua O, ta xác định mặt phẳng (O; Δ) và trong mặt phẳng này kẻ OH ⊥ Δ. Độ dài OH chính là khoảng cách từ O đến Δ.
b) Để tính khoảng cách giữa đường thẳng a và mp(P) song song với (P), ta lấy một điểm M bất kì thuộc đường thẳng a. Khoảng cách MN từ điểm M đến mp(P) chính là khoảng cách giữa đường thẳng và mp(P) song song với a.
c) Để tính khoảng cách giữa hai mp(P) và (P') song song với nhau, ta lấy một điểm M thuộc (P) và tìm khoảng cách MH từ điểm M đến mp(P').

\(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=45^0\Rightarrow AC=SA=a\sqrt{2}\)
\(\Rightarrow AB=a\)
Gọi N là trung điểm SA \(\Rightarrow NM||SB\Rightarrow SB||\left(DMN\right)\)
\(\Rightarrow d\left(DM;SB\right)=d\left(SB;\left(DMN\right)\right)=d\left(B;\left(DMN\right)\right)\)
Mà M là trung điểm AB \(\Rightarrow d\left(B;\left(DMN\right)\right)=d\left(A;\left(DMN\right)\right)\)
Từ A kẻ AH vuông góc DM \(\Rightarrow DM\perp\left(NAH\right)\)
Trong mp (NAH), từ A kẻ \(AK\perp NH\Rightarrow AK=d\left(A;\left(DMN\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{AM^2}+\dfrac{1}{AD^2}\Rightarrow AH=\dfrac{AM.AD}{\sqrt{AM^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
\(\dfrac{1}{AK^2}=\dfrac{1}{AN^2}+\dfrac{1}{AH^2}\Rightarrow AK=\dfrac{AN.AH}{\sqrt{AN^2+AH^2}}=\dfrac{a\sqrt{7}}{7}\)
Dựa vào bài học, chúng ta sẽ có các định nghĩa sau đây:
1: Khoảng cách từ một điểm M đến một đường thẳng a là khoảng cách giữa M và hình chiếu H của M trên a.
2: Khoảng cách từ điểm M đến mặt phẳng (P) là khoảng cách giữa M và hình chiếu H của M trên (P)
3: Khoảng cách giữa đường thẳng a và mặt phẳng (P) song song với a là khoảng cách từ một điểm bất kì trên a đến (P).
4: Khoảng cách giữa hai mặt phẳng song song (P) và (Q) là khoảng cách từ một điểm bất kì thuộc mặt phẳng này đến mặt phẳng kia.
Chúng ta có đường vuông góc bao giờ cũng là đường ngắn nhất nối giữa hai điểm bất kì trong hai mặt phẳng phân biệt.
Do đó: Khoảng cách giữa hai mặt phẳng là khoảng cách nhỏ nhất giữa hai điểm bất kì nằm trong hai mặt phẳng đó