Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a)(4x-3)(3x+2)-(6x+1)(2x-5)+1
=12x2-x-6-12x2+28x+5+1
=27x
b)(3x+4)2+(4x-1)2+(2+5x)(2-5x)
=9x2+24x+16+16x2-8x+1+4-25x2
=16x+21
c)(2x+1)(4x2-2x+1)+(2-3x)(4+6x+9x2)-9
=8x3+1+8-27x3-9
=-19x3
Bài 2:
a)3x(x-4)-x(5+3x)=-34
=>3x2-12x-3x2-5x=-34
=>-17x=-34
=>x=2
Vậy x=2
b)(3x+1)2+(5x-2)2=34(x+2)(x-2)
=>9x2+6x+1+25x2-20x+4=34(x2-4)
=>34x2-14x+5-34x2+136=0
=>-14x+141=0
=>-14x=-141
=>x=\(\frac{141}{14}\)
Vậy x=\(\frac{141}{14}\)
c)x3+3x2+3x+28=0
=>x3-x2+7x+4x2-4x+28=0
=>x(x2-x+7)+4(x2-x+7)=0
=>(x+4)(x2-x+7)=0
\(\Rightarrow\left[\begin{array}{nghiempt}x+4=0\\x^2-x+7=0\left(2\right)\end{array}\right.\)
\(\Rightarrow\left[\begin{array}{nghiempt}x=-4\\\left(2\right)\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{27}{4}>0\end{array}\right.\)
=>(2) vô nghiệm
Vậy x=-4

a: \(\Leftrightarrow4\left(x^2+60+17x\right)\left(x^2+60+16x\right)=3x^2\)
\(\Leftrightarrow4\cdot\left[\left(x^2+60\right)^2+33x\left(x^2+60\right)+272x^2\right]=3x^2\)
=>4(x^2+60)^2+132x(x^2+60)+1085x^2=0
=>4(x^2+60)^2+62x(x^2+60)+70x(x^2+60)+1085x^2=0
=>2(x^2+60)(2x^2+120+31x)+35x(2x^2+120+31x)=0
=>(2x^2+120+35x)(2x^2+31x+120)=0
=>\(x\in\left\{\dfrac{-35\pm\sqrt{265}}{4};-\dfrac{15}{2};-8\right\}\)
b: Đặt x^2-3x=a
Phương trình sẽ là \(\dfrac{1}{a+3}+\dfrac{2}{a+4}=\dfrac{6}{a+5}\)
\(\Leftrightarrow\dfrac{a+4+2a+6}{\left(a+3\right)\left(a+4\right)}=\dfrac{6}{a+5}\)
=>(3a+10)(a+5)=6(a^2+7a+12)
=>6a^2+42a+72=3a^2+15a+10a+50
=>3a^2+17a+22=0
=>x=-2 hoặc x=-11/3

chẳng ai giải, thôi mình giải vậy!
a) Đặt \(y=x^2+4x+8\),phương trình có dạng:
\(t^2+3x\cdot t+2x^2=0\)
\(\Leftrightarrow t^2+xt+2xt+2x^2=0\)
\(\Leftrightarrow t\left(t+x\right)+2x\left(t+x\right)=0\)
\(\Leftrightarrow\left(2x+t\right)\left(t+x\right)=0\)
\(\Leftrightarrow\left(2x+x^2+4x+8\right)\left(x^2+4x+8+x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-4\end{cases}}\)vậy tập nghiệm của phương trình là:S={-2;-4}
b) nhân 2 vế của phương trình với 12 ta được:
\(\left(6x+7\right)^2\left(6x+8\right)\left(6x+6\right)=72\)
Đặt y=6x+7, ta được:\(y^2\left(y+1\right)\left(y-1\right)=72\)
giải tiếp ra ta sẽ được S={-2/3;-5/3}
c) \(\left(x-2\right)^4+\left(x-6\right)^4=82\)
S={3;5}
d)s={1}
e) S={1;-2;-1/2}
f) phương trình vô nghiệm

Đáp án :
1- C
2-A
3-B
4-D
5-
6-D
7-A
8-B
9-
10-D
11-
12-B
13-B
14-C
15-
16-D
17-
18-D
19-D
20-D
Câu 1:Trong các pt sau đây, pt nào là pt bậc nhất một ẩn
A.x-1=x+2 B.(x-1)(x+2)=0 C.ax+b=0 D.2x+1=3x+5
Câu2: x=-2 là nghiệm của pt nào ?
A.3x-1=x-5 B.2x-1=x+3 C.x-3=x-2 D.3x+5=-x-2
Câu 3: x-4 là nghiệm của pt
A.3x-1=x-5 B.2x-1=x+3 C.x-3=x-2 D.3x+5=-x-2
Câu 4: Pt x+9=9+x có nghiệm là
A.S=R B.S=9 C.S rỗng D. S thuộc R
Câu 5: cho 2pt: x(x-1)=0(1) và 3x-3=0 (2)
A.(1) tương đương (2) B.(1) là hệ quả của pt (2)
C.(2) là hệ quả của pt (1) D. Cả 3 sai
Câu 6: Pt x2x2=-4 có nghiệm là
A. Một nghiệm x=2 B. Có hai nghiệm x=-2;x=2
C.Mộe nghiệm x=-2 D. Vô nghiệm
Câu 7: Chọn kết quả đúng
A. x2=3xx2=3x <=> x(x-3) =0 B.(x−1)2−25(x−1)2−25= 0 <=> x=6
C. x2x2 =9 <=> x=3 D.x2x2 =36<=> x=-6
Câu 8: Cho biết 2x-4=0. Tính 3x-4=
A. 0 B. 2 C. 17 D. 11
Câu 9: Pt (2x-3)(3x-2)=6x(x-50)+44 có tập nghiệm
A. S={2}{2} B. S={2;−3}{2;−3} C. S={2;13}{2;13} D. S={2;0;3}{2;0;3}
Câu 10: Pt 3x-5x+5=-8 có nghiệm là
A. x=-2323 B. x=2323 C. x=4 D. Kết quả khác
Câu 11: Giá trị của b để pt 3x+6=0 có nghiệm là x=-2
A.4 B. 5 C. 6 D. Kết quả khác
Câu 12: Pt 2x+k=x-1 nhận x=2 là nghiệm khi
A. k=3 B. k=-3 C. k=0 D.k=1
Câu 13: Pt m(x-1)=5-(m-1)x vô nghiệm nếu
A. m=1414 B. m=1212 C.m=3434 D. m=1
Câu 14: Pt x2x2 -4x+3=0 có nghiệm là
A. {1;2}{1;2} B. {2;3}{2;3} C. {1;3}{1;3} D. {2;4}{2;4}
Câu 15: Pt x2x2 -4x+4=9(x−2)2(x−2)2 có nghiệm là
A. {2}{2} B. {−2;2}{−2;2} C. {−2}{−2} D. Kết quả khác
Câu 16: Pt 1x+2+3=3−xx−21x+2+3=3−xx−2 có nghiệm
A.1 B. 2 C. 3 D. Vô nghiệm
Câu 17: Pt x+2x−2−2x(x−2)=1xx+2x−2−2x(x−2)=1x có nghiệm là
A. {−1}{−1} B. {−1;3}{−1;3} C. {−1;4}{−1;4} D. S=R
Câu 18: Pt x2(x−3)+x2(x+1)=2x(x+1)(x+3)x2(x−3)+x2(x+1)=2x(x+1)(x+3) có nghiệm là
A. -1 B. 1 C. 2 D. Kết quả khác
Câu 19: Pt x2+2xx2+1−2x=0x2+2xx2+1−2x=0 có nghiệm là
A. -2 B.3 C. -2 và 3 D. kết quả khác
Câu 20: ĐKXĐ của Pt 3x+2x+2+2x−11x2−4−32−x3x+2x+2+2x−11x2−4−32−x là
A. x−23−23; x≠112≠112 B. x≠≠2 C. x>0 D. x≠≠ 2 và x≠≠ -2

b/ \(3-100x+8x^2=8x^2+x-300\)
\(\Leftrightarrow-101x=-303\)
\(\Rightarrow x=3\)
c/ \(5\left(5x+2\right)-10\left(8x-1\right)=6\left(4x+2\right)-150\)
\(\Leftrightarrow25x+10-80x+10=24x+12-150\)
\(\Leftrightarrow-79x=-158\)
\(\Rightarrow x=2\)
d/ \(3\left(3x+2\right)-\left(3x+1\right)=12x+10\)
\(\Leftrightarrow9x+6-3x-1=12x+10\)
\(\Leftrightarrow-6x=5\)
\(\Rightarrow x=-\frac{5}{6}\)
e/ \(30x-6\left(2x-5\right)+5\left(x+8\right)=210+10\left(x-1\right)\)
\(\Leftrightarrow30x-12x+30+5x+40=210+10x-10\)
\(\Leftrightarrow13x=130\)
\(\Rightarrow x=10\)
\(A=x^2-4x+1=\left(x-2\right)^2-3\ge-3\)
\(\Rightarrow A_{min}=-3\) khi \(x=2\)
\(B=4x^2+4x+11=\left(2x+1\right)^2+10\ge10\)
\(\Rightarrow B_{min}=10\) khi \(x=-\frac{1}{2}\)
\(C=\left(x-1\right)\left(x+6\right)\left(x+2\right)\left(x+3\right)=\left(x^2+5x-6\right)\left(x^2+5x+6\right)\)
\(=\left(x^2+5x\right)^2-36\ge-36\)
\(\Rightarrow C_{min}=-36\) khi \(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
\(D=-x^2-8x-16+21=21-\left(x+4\right)^2\le21\)
\(\Rightarrow C_{max}=21\) khi \(x=-4\)
\(E=-x^2+4x-4+5=5-\left(x-2\right)^2\le5\)
\(\Rightarrow E_{max}=5\) khi \(x=2\)
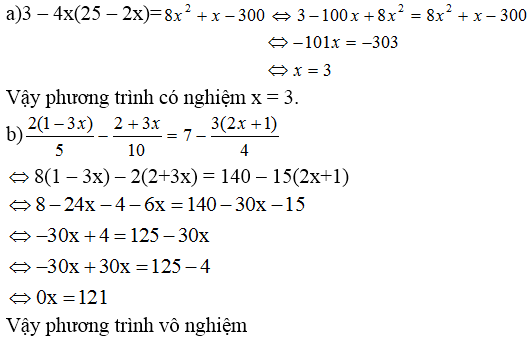

c
(6x9 - 2x6 + 8x3) : 2x3
= (6x9 : 2x3) + (-2x6 : 2x3) + (8x3 : 2x3)
= (3x6 - x3 + 4)
=> Chọn C. (3x6 - x3 + 4)