Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BT1.
Ta có: \(2009^{20}=2009^{10}\times2009^2\)và \(20092009^{10}=2009^{10}\times10001^{10}\)
Rõ ràng \(2009^2< 10001^{10}\\ \Rightarrow2009^{10}\times2009^2< 2009^{10}\times10001^{10}\\ \Rightarrow2009^{20}< 20092009^{10}\left(đpcm\right)\)
BT9. Bn xem lại đề bài đi. \(x^2+x+1\) luôn lớn hơn 0 mà bn.
BT3.
Giả sử \(M\in N\)
Nên:
\(\left\{{}\begin{matrix}\dfrac{x}{x+y+z}\in N\\\dfrac{y}{y+x+t}\in N\\\dfrac{z}{z+t+y}\in N\\\dfrac{t}{t+z+x}\in N\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x⋮x+y+z\\y⋮y+x+t\\z⋮z+t+y\\t⋮t+z+x\end{matrix}\right.\)
Vì \(x,y,z,t\in N\)*\(\Rightarrow x,y,z,t>0\)\(\Rightarrow\left\{{}\begin{matrix}x>x+y+z\\y>x+y+t\\z>y+z+t\\t>x+z+t\end{matrix}\right.\)(vô lí)
Vậy rõ ràng điều giả sử là vô lí. Nên \(M\notin N\left(đpcm\right)\)
Mình chỉ giúp đc đến đây thôi, mong bn thông cảm
Ngoài ra, chúc bn học tốt nhé![]()
![]()
![]()
![]()
![]()
Bài toán 2.
Ta có: \(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+....+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(=\dfrac{2009-1}{1}+\dfrac{2009-2}{2}+\dfrac{2009-3}{3}+...+\dfrac{2009-2008}{2008}\)
\(=2009-1+\dfrac{2009}{2}-1+\dfrac{2009}{3}-1+....+\dfrac{2009}{2008}-1\)
\(=2009+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{....1}{2008}\right)-1.2008\)
\(=\left(2009-2008\right)+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=1+2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+....+\dfrac{1}{2008}\right)\)
\(=2009\left(\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
=\(2009.A\)
Do đó, tỉ số \(\dfrac{A}{B}=\dfrac{A}{2009.A}=\dfrac{1}{2009}\)

a: Xét ΔEFI và ΔEMI có
EF=EM
FI=MI
EI chung
Do đó: ΔEFI=ΔEMI
b: Ta có: ΔEFM cân tại E
mà EI là đường trung tuyến
nên EI là đường cao
c: Xét ΔEFK và ΔEMK có
EF=EM
\(\widehat{FEK}=\widehat{MEK}\)
EK chung
Do đó: ΔEFK=ΔEMK
Suy ra: FK=MK
Xét ΔNFD và ΔNMK có
NF=NM
\(\widehat{NFD}=\widehat{NMK}\)
FD=MK
Do đó: ΔNFD=ΔNMK
Suy ra: \(\widehat{FND}=\widehat{MNK}\)
=>\(\widehat{FND}+\widehat{FNM}=180^0\)
hay M,N,D thẳng hàng

Đặt \(\dfrac{x}{2015}=\dfrac{y}{2016}=\dfrac{z}{2017}=k\)
\(\Rightarrow\left\{{}\begin{matrix}x=2015k\\y=2016k\\z=2017k\end{matrix}\right.\)
\(\Rightarrow\left(x-z\right)^3\div\left[\left(x-y\right)^2\left(y-z\right)\right]\)
\(=\left(2015k-2017k\right)^3\div\left[\left(2015k-2016k\right)^2\left(2016k-2017k\right)\right]\)
\(=\left(-2k\right)^3\div\left[-k^2\left(-k\right)\right]\)
\(=-8k^3\div\left(-k\right)^3\)
\(=8\)
Vậy \(\left(x-z\right)^3\div\left[\left(x-y\right)^2\left(y-z\right)\right]=8\)

ta có x=9+y
thay x=9+y vào biểu thức B ta có:
B=\(\dfrac{7\left(9+y\right)-9}{6\left(9+y\right)+y}\)+\(\dfrac{7\left(9+y\right)+9}{8\left(9+y\right)-y}\)
B=\(\dfrac{63+7y-9}{54+6y+y}\)+\(\dfrac{63+7y+9}{72+8y-y}\)
B=\(\dfrac{54+7y}{54+7y}\)+\(\dfrac{72+7y}{72+7y}\)
B=1+1
B=2
![]()

Ta có: a=512.46=512.(22)6=512.212=(5.2)12=1012
(=1000000000000)
Vậy số chữ số của a là 12.
512.46=512.(22)6 (Lũy thừa của lũy thừa đó bn)
=512.22.6=512.212=(5.2)12=1012
=>1012=1000...000 có 12 số 0 và 1 số 1 nên số nay có 13 chữ số
Thanks!

Ta có: x và y là 2 đl tlt nên \(\dfrac {x1}{y1} \)=\(\dfrac{x2}{y2}\) .
Thay số: \(\dfrac {6}{y1} \)=\(\dfrac{-9}{y2}\)=\(\dfrac{6-(-9)}{y1-y2}\)=\(\dfrac{15}{10} \)=1,5
=>y1=\(\dfrac{6}{1,5} \)= 4; y2=\(\dfrac{-9}{1,5} \)= -6
Vậy y1+y2=4+(-6)=-2

Ta đánh giá phương trình ở đề bài:
Dễ thấy (x-3y)2, (y-1)2, (x+z)2 đều lớn hơn hoặc bằng 0 với mọi giá trị của biến. Do vậy tổng của chúng bằng 0 khi và chỉ khi:\(\left\{{}\begin{matrix}\left(x-3y\right)^2=0\\\left(y-1\right)^2=0\\\left(x+z\right)^2=0\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=3y\\y=1\\x=-z\end{matrix}\right.\)<=>\(\left\{{}\begin{matrix}x=3\\y=1\\z=-3\end{matrix}\right.\)
=>A=3x+2y+z=3.3+2.1-3=8
ta có:(x-3y)2>=0
(y+1)2>=0
(x+z)2>=0
=>\(\begin{matrix}\left(x-3y\right)^2=0&=>x-3y=0&=>x=3y&=>x=3&\\\left(y-1\right)^2=0&=>y-1=0&=>y=1&=>y=1&\\\left(x+z\right)^2=0&=>x+z=0&=>z=-x&=>z=-3&\end{matrix}\)
thay x,y,z vào biểu thức A ta có:
A=3.3+2.1+(-3)
A=3+2-3
A=2![]()
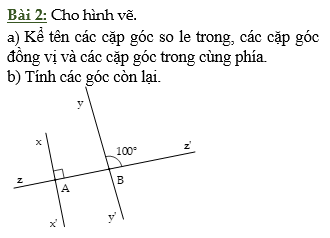



 Giải giùm em nhanh ạ. Vì ko có time nên thòng cảm cho em ko đasnh máy đặc chỉ chụp thui
Giải giùm em nhanh ạ. Vì ko có time nên thòng cảm cho em ko đasnh máy đặc chỉ chụp thui





a:So le trong: \(\widehat{xAB};\widehat{y'BA}\);\(\widehat{x'AB};\widehat{yBA}\)
Đồng vị: \(\widehat{xAB};\widehat{yBz'}\)
\(\widehat{x'AB};\widehat{y'Bz'}\)
\(\widehat{zAx};\widehat{yBz}\)
\(\widehat{x'Az};\widehat{y'Bz'}\)