TH
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
B1
1
B1
17 tháng 8 2017
 |
Đề bài: tính diện tích phần bôi đen (đơn vị cm)
Đáp án: Lấy diện tích hình chữ nhật trừ đi diện tích hai hình tròn rồi chia đôi. Sau đó bôi đen góc nhọn phía dưới bên trái.
 |
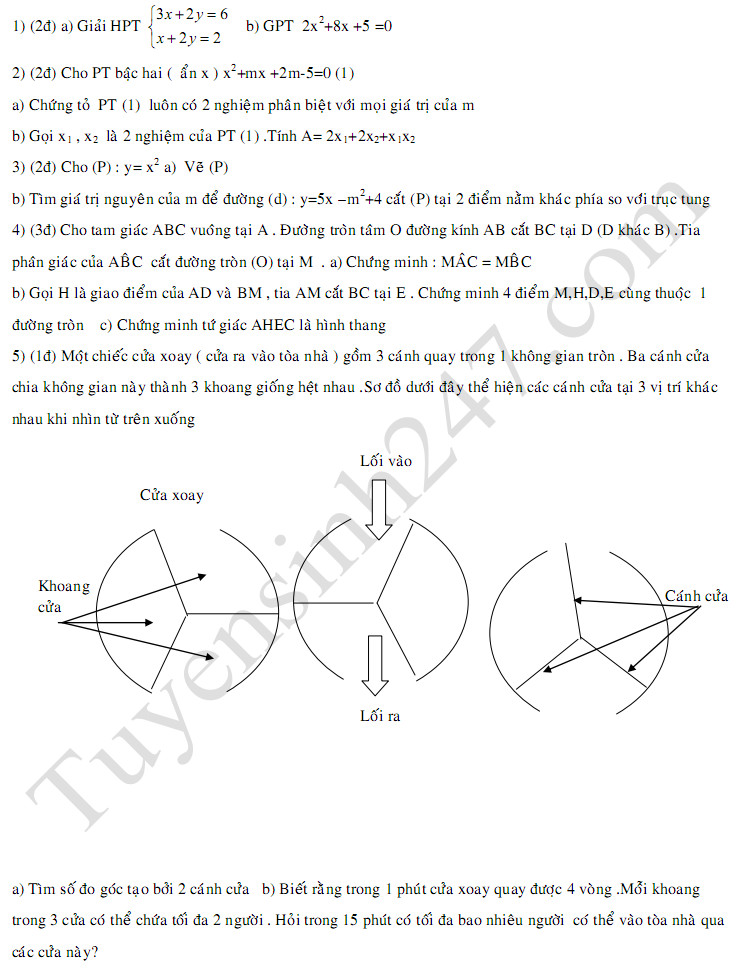
Điều cần làm là tính diện tích hình màu đỏ và nó được tính như sau:
1. Diện tích góc màu xanh = (Diện tích hình vuông 10*10 - diện tích hình tròn) chia cho 4
2. Diện tích cung màu vàng = diện tích cung hình tròn - diện tích tam giác ABD
- Diện tích tam giác ABD khá đơn giản khi biết cạnh AB = 5 và góc ACB có tang = 1/2.
- Trong đó diện tích cung tròn cũng dễ dàng tìm ra khi biết được góc của cung là (180-2*góc CAB).
3. Vậy diện tích phần màu đỏ = Diện tích tam giác LAM - diện tích cung màu vàng - diện tích góc màu xanh.
DH
= ....................
1
26 tháng 11 2017
TA CÓ :\(5+2\sqrt{6}=\left(\sqrt{3}+\sqrt{2}\right)^2\)
\(\Rightarrow\frac{\sqrt{5+2\sqrt{6}}}{\sqrt{3}+\sqrt{2}}+2014=\frac{\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}}{\sqrt{3}+\sqrt{2}}+2014\)
\(=1+2014=2015\)
Vậy giá trị biểu thức là 2015.
UK
10 tháng 11 2017
a) Từ gt, suy ra
\(\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x^2-xy+y^2\right)+\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4=0\)
\(\Leftrightarrow\left(x^2-xy+y^2\right)\left(x+y+2\right)+\left(x+y+2\right)^2=0\)
\(\Leftrightarrow\dfrac{1}{2}\left(x+y+2\right)\left(2x^2-2xy+2y^2+2x+2y+4\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}\left(x+y+2\right)\left[\left(x-y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2+2\right]=0\)
Do đó: \(x+y+2=0\Leftrightarrow x+y=-2\)
Mặt khác \(xy>0\Rightarrow x< 0;y< 0\)
Áp dụng AM-GM, ta có
\(\sqrt{\left(-x\right)\left(-y\right)}\le\dfrac{\left(-x\right)+\left(-y\right)}{2}=1\) nên \(xy\le1\)\(\Rightarrow\dfrac{-2}{xy}\le-2\)
\(M=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{x+y}{xy}\le-2\)
GTLN của M là -2 khi x=y=-1
UK
10 tháng 11 2017
Áp dụng Cauchy-Schwarz dạng Engel, ta có
\(VT=\dfrac{a^6}{a^3+a^2b+b^2a}+\dfrac{b^6}{b^3+b^2c+c^2b}+\dfrac{c^6}{c^3+c^2a+ca^2}\ge\dfrac{\left(a^3+b^3+c^3\right)^2}{a^3+b^3+c^3+ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)}\)
Mặt khác: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-ab+b^2\ge ab\Leftrightarrow a^3+b^3\ge ab\left(a+b\right)\)
Tương tự: \(b^3+c^3\ge bc\left(b+c\right);c^3+a^3\ge ca\left(c+a\right)\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)\ge ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\)
\(3\left(a^3+b^3+c^3\right)\ge a^3+b^3+c^3+ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\)
\(\Rightarrow\dfrac{\left(a^3+b^3+c^3\right)^2}{a^3+b^3+c^3+ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)}\ge\dfrac{a^3+b^3+c^3}{3}\)
Vậy ta có đpcm. Đẳng thức xảy ra khi và chỉ khi a=b=c
Ko đăng câu hỏi linh tinh
Hok tốt
# MissyGirl #
minh an nham day ma