
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a)\hept{\begin{cases}\text{Ta có:}\widehat{A_4}=\widehat{B_2}=110^0\\\text{Mà chúng so le trong}\end{cases}}\)
\(\Rightarrow a//b\)
\(b)\hept{\begin{cases}\text{Ta có:}c\perp a\left(gt\right)\\\text{Mà }a//b\left(cmt\right)\end{cases}}\)
\(\Rightarrow c\perp b\)
\(c)\text{Ta có:}\widehat{B_1}+\widehat{B_2}=180^0\left(\text{kề bù}\right)\)
\(\Rightarrow\widehat{B_1}=180^0-\widehat{B_2}\)
\(\Rightarrow\widehat{B_1}=180^0-110^0=70^0\)
\(\text{Ta có:}\widehat{B_1}=\widehat{B_3}=70^0\left(\text{đối đỉnh}\right)\)
\(\text{Ta có:}\widehat{B_3}=\widehat{C_3}\left(\text{Đồng vị}\right)\)
\(\Rightarrow\widehat{B_3}=\widehat{C_3}=70^0\)
a) Ta có: {ˆA4=110∘ˆB2=110∘⇒ˆA4=ˆB2=110∘{A4^=110∘B2^=110∘⇒A4^=B2^=110∘.
Mà hai góc ờ vị trí so le trong ⇒⇒ a//ba//b.
b) Ta có: {c⊥aa//b⇒c⊥b{c⊥aa//b⇒c⊥b
c) Vì a//b⇒ˆA4+ˆB1=180∘a//b⇒A4^+B1^=180∘
Mà hai góc ở vị trí trong cùng phía ⇒ˆB1=180∘−ˆA4=70∘⇒B1^=180∘−A4^=70∘.
Vì b⊥cb⊥c; e⊥ce⊥c và b//eb//e
⇒ˆB2=ˆC2=110∘⇒B2^=C2^=110∘ (hai góc ở vị trí đồng vị)
Ta có ˆC2C2^ và ˆC3C3^ là hai góc kề bù ⇒ˆC2+ˆC3=180∘⇒C2^+C3^=180∘
⇒ˆC3=180∘−ˆC2=70∘⇒C3^=180∘−C2^=70∘.

Kẻ tia CxCx là tia phân giác của ˆACDACD^ và DyDy là tia phân giác của ˆBDCBDC^, hai tia CxCx và DyDy cắt nhau tại EE.
ˆC1=ˆC2=60∘C1^=C2^=60∘ và ˆD1=ˆD2=30∘D1^=D2^=30∘
Kẻ tia Ez//m//nEz//m//n, tính ˆE1=60∘E1^=60∘ và ˆE2=30∘E2^=30∘
Suy ra ˆCED=90∘CED^=90∘.
Kẻ tia CxCx là tia phân giác của \widehat{A C D}ACD và DyDy là tia phân giác của \widehat{B D C}BDC, hai tia CxCx và DyDy cắt nhau tại EE.
\widehat{C_1}=\widehat{C_2}=60^{\circ}C1=C2=60∘ và \widehat{D_1}=\widehat{D_2}=30^{\circ}D1=D2=30∘
Kẻ tia Ez / / m // nEz//m //n, tính \widehat{E_1}=60^{\circ}E1=60∘ và \widehat{E_2}=30^{\circ}E2=30∘
Suy ra \widehat{CED}=90^{\circ}CED=90∘.

\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

Lời giải:
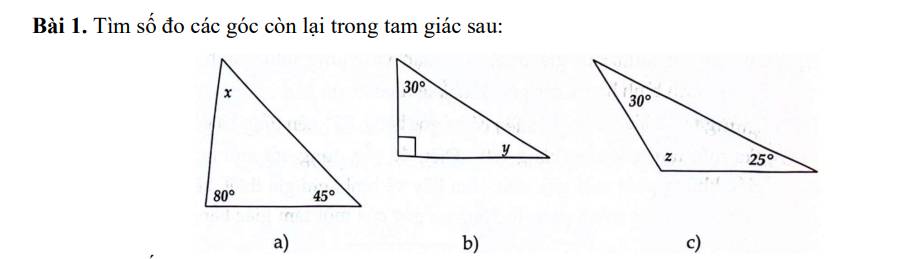
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$

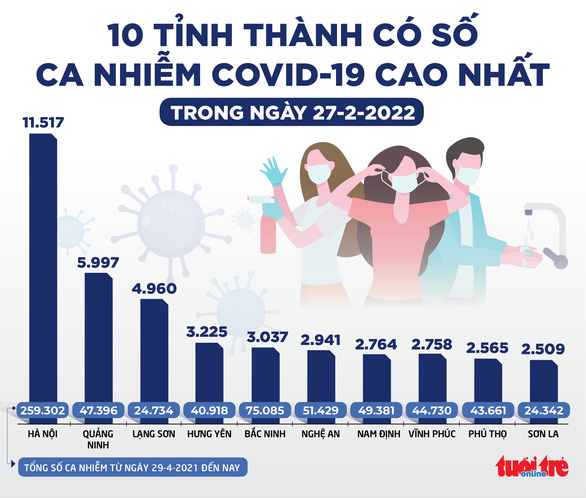
a. Những tỉnh thành phố có ca nhiễm hơn 2800 ca: Nghệ An, Bắc Ninh, Hưng Yên, Lạng Sơn, Quảng Ninh, Hà Nội.
b. Tỉnh có số ca nhiễm Covid 19 cao nhất là: Hà Nội

Xét 2 tam giác ABC và MNP có:
AB=MN (gt)
\(\widehat {BAC} = \widehat {NMP}\) (gt)
AC=MP (gt)
Vậy \(\Delta ABC = \Delta MNP\)(c.g.c)
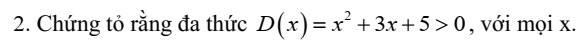


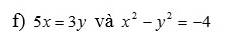

`Answer:`
\(D\left(x\right)=x^2+3x+5\)
\(=x^2+3x+\frac{9}{4}+\frac{11}{4}\)
\(=\left(x+\frac{3}{2}\right)^2+\frac{11}{4}\)
Mà \(\left(x+\frac{3}{2}\right)^2\ge0\forall x\)
\(\Rightarrow D\left(x\right)=\left(x+\frac{3}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}>0\)
Vậy `D(x)=x^2 +3x+5>0` với mọi `x`